题目内容
设数列{an}的前n项和为Sn,令Tn=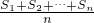 ,称Tn为数列a1,a2,…,an的“理想数”.已知a1,a2,…,a500的“理想数”为1002,那么数列3,a1,a2,….a500的“理想数”为
,称Tn为数列a1,a2,…,an的“理想数”.已知a1,a2,…,a500的“理想数”为1002,那么数列3,a1,a2,….a500的“理想数”为
- A.1005
- B.1003
- C.1002
- D.999
B
分析:由题意可知n•Tn=(S1+S2+…+Sn),设新的理想数为Tx,根据理想数的公式可知 501×Tx=3×501+500×T500进而求得答案.
解答: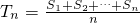 ,∴n•Tn=(S1+S2+…+Sn),
,∴n•Tn=(S1+S2+…+Sn),
∵T500=1002,设新的理想数为Tx
501×Tx=3×501+500×T500
∴Tx=3+ ×500×T500=3+500×2=1003,
×500×T500=3+500×2=1003,
故选B.
点评:本题主要考查了数列的求和问题.考查了学生根据已知条件解决实际问题的能力,考查了学生的创造性的能力.
分析:由题意可知n•Tn=(S1+S2+…+Sn),设新的理想数为Tx,根据理想数的公式可知 501×Tx=3×501+500×T500进而求得答案.
解答:
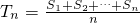 ,∴n•Tn=(S1+S2+…+Sn),
,∴n•Tn=(S1+S2+…+Sn),∵T500=1002,设新的理想数为Tx
501×Tx=3×501+500×T500
∴Tx=3+
 ×500×T500=3+500×2=1003,
×500×T500=3+500×2=1003,故选B.
点评:本题主要考查了数列的求和问题.考查了学生根据已知条件解决实际问题的能力,考查了学生的创造性的能力.

练习册系列答案
相关题目