题目内容
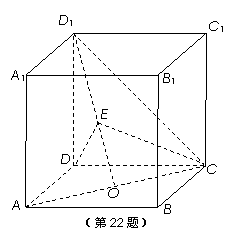
正方体![]() 中,O是AC的中点,E是线段D1O上一点,且D1E=λEO.
中,O是AC的中点,E是线段D1O上一点,且D1E=λEO.
(1)若λ=1,求异面直线DE与CD1所成角的余弦值;
(2)若平面CDE⊥![]() 平面CD1O,求λ的值.
平面CD1O,求λ的值.
【解】(1)不妨设正方体的棱长为1,以![]() 为单位正交基底建立如图所示的空间直角坐标系
为单位正交基底建立如图所示的空间直角坐标系![]() .则A(1,0,0),
.则A(1,0,0),![]() ,
,![]() ,D1(0,0,1),
,D1(0,0,1),
E![]() ,
,
于是![]() ,
,![]() .
.
由cos![]() =
=![]() =
=![]() .[来源:Zxxk.Com]
.[来源:Zxxk.Com]
所以异面直线AE与CD1所成角的余弦值为![]() . ……………………5分
. ……………………5分
(2)设平面CD1O的向量为m=(x1,y1,z1),由m·![]() =0,m·
=0,m·![]() =0
=0
得 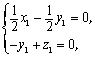 取x1=1,得y1=z1=1,即m=(1,1,1) . ………………7分
取x1=1,得y1=z1=1,即m=(1,1,1) . ………………7分
由D1E=λEO,则E![]() ,
,![]() =
=![]() .[来源:学科网ZXXK]
.[来源:学科网ZXXK]
又设平面CDE的法向量为n=(x2,y2,z2),由n·![]() =0,n·
=0,n·![]() =0.
=0.
得 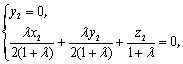 取x2=2,得z2=-λ,即n=(-2,0,λ) .
取x2=2,得z2=-λ,即n=(-2,0,λ) .
因为平面CDE⊥平面CD1F,所以m·n=0,得λ=2. …………………10分

练习册系列答案
相关题目
 (2012•扬州模拟)如图:在正方体ABCD-A1B1C1D1中,O是AC的中点,E是线段D1O上一点,且
(2012•扬州模拟)如图:在正方体ABCD-A1B1C1D1中,O是AC的中点,E是线段D1O上一点,且 (1)若λ=1,求异面直线DE与CD1所成角的余弦值;
(1)若λ=1,求异面直线DE与CD1所成角的余弦值;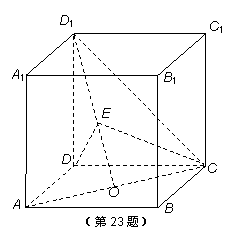 (1)若λ=1,求异面直线DE与CD1所成角的余弦值;
(1)若λ=1,求异面直线DE与CD1所成角的余弦值;