题目内容
求函数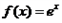
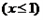 的切线与坐标轴围成的三角形面积的最大值。
的切线与坐标轴围成的三角形面积的最大值。
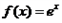
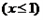 的切线与坐标轴围成的三角形面积的最大值。
的切线与坐标轴围成的三角形面积的最大值。解:∵过函数图象上任意一点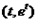 的切线方程是
的切线方程是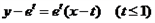 ,
,
∴切线在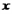 轴和
轴和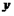 轴上的截距分别为
轴上的截距分别为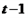 ,
,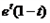 .
.
∴切线与坐标轴围成的三角形面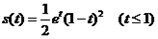 .
.
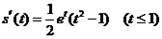 ,
,
由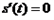 得
得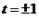 .
.
 当
当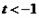 时,
时,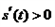 ,
,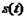 为增函数;
为增函数;
当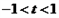 时,
时,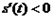 ,
,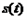 为减函数.
为减函数.

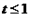 ,
,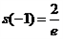 ,
, 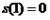
所以函数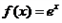
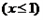 的切线与坐标轴围成的三角形面积的最大值为
的切线与坐标轴围成的三角形面积的最大值为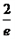 .
.
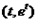 的切线方程是
的切线方程是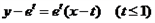 ,
,∴切线在
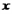 轴和
轴和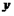 轴上的截距分别为
轴上的截距分别为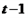 ,
,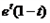 .
.∴切线与坐标轴围成的三角形面
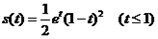 .
. 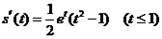 ,
,由
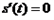 得
得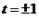 .
. 当
当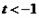 时,
时,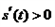 ,
,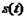 为增函数;
为增函数;当
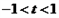 时,
时,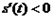 ,
,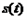 为减函数.
为减函数.
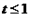 ,
,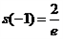 ,
, 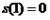
所以函数
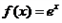
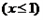 的切线与坐标轴围成的三角形面积的最大值为
的切线与坐标轴围成的三角形面积的最大值为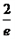 .
.
练习册系列答案
相关题目