题目内容
设数列{an}的前n项和为Sn,且对任意正整数n,an+Sn=32.(1)求数列{an}的通项公式
(2)设数列{log2an}的前n项和为Tn,对数列{Tn},从第几项起Tn<-18?
【答案】分析:(I)利用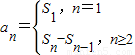 即可得出;
即可得出;
(II)利用(I)可得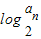 ,再利用等差数列的前n项和公式即可得出.
,再利用等差数列的前n项和公式即可得出.
解答:解:(Ⅰ)当n=1,a1=16,
当n>1,an+Sn=32,an-1+Sn-1=32,两式相减得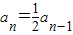 .
.
数列{an}是首项为16,公比为 的等比数列,
的等比数列,
∴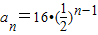 =25-n.
=25-n.
(Ⅱ)∵log2an=5-n,
∴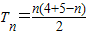 =
=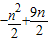 <-18,解得n>12.
<-18,解得n>12.
∴从13项起满足Tn<-18.
点评:熟练掌握利用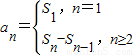 得出an、等差数列的前n项和公式、对数的运算性质等是解题的 关键.
得出an、等差数列的前n项和公式、对数的运算性质等是解题的 关键.
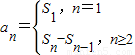 即可得出;
即可得出;(II)利用(I)可得
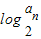 ,再利用等差数列的前n项和公式即可得出.
,再利用等差数列的前n项和公式即可得出.解答:解:(Ⅰ)当n=1,a1=16,
当n>1,an+Sn=32,an-1+Sn-1=32,两式相减得
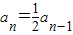 .
.数列{an}是首项为16,公比为
 的等比数列,
的等比数列,∴
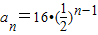 =25-n.
=25-n.(Ⅱ)∵log2an=5-n,
∴
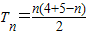 =
=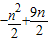 <-18,解得n>12.
<-18,解得n>12.∴从13项起满足Tn<-18.
点评:熟练掌握利用
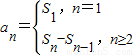 得出an、等差数列的前n项和公式、对数的运算性质等是解题的 关键.
得出an、等差数列的前n项和公式、对数的运算性质等是解题的 关键. 
练习册系列答案
相关题目