题目内容
已知数列{an}的通项公式是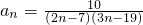 ,则该数列的最大项和最小项的和为
,则该数列的最大项和最小项的和为
- A.

- B.
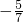
- C.
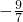
- D.-1
D
分析:根据通项公式的特点,令f(n)=(2n-7)(3n-19)(n∈N+),判断出各项的符号,利用单调性再求最大项和最小项的值.
解答:令f(n)=(2n-7)(3n-19)(n∈N+),
解f(n)>0得,n< 或 n>
或 n> ;解f(n)<0得,
;解f(n)<0得, <n<
<n< ,
,
∴当n< 或n>
或n> 时,an>0;当
时,an>0;当  <n<
<n< 时,an<0,
时,an<0,
∵f(n)=(2n-7)(3n-19)=6n2-59n+133
∴当n=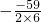 =
=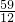 时,f(n)有最小值,且在(
时,f(n)有最小值,且在(  ,
, )上递减
)上递减
∵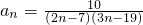 ,并且n∈N+,
,并且n∈N+,
∴当n=3时,an有最大值为a3=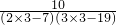 =1,
=1,
当n=6时,an有最小值为a6=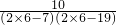 =-2,
=-2,
∴该数列的最大项和最小项的和为-1.
故选D.
点评:本题是以函数的角度来求数列中的最大项和最小项问题,一定要注意各项的符号;构造关于n的二次函数,利用函数的单调性来求,但是n只取正整数.
分析:根据通项公式的特点,令f(n)=(2n-7)(3n-19)(n∈N+),判断出各项的符号,利用单调性再求最大项和最小项的值.
解答:令f(n)=(2n-7)(3n-19)(n∈N+),
解f(n)>0得,n<
 或 n>
或 n> ;解f(n)<0得,
;解f(n)<0得, <n<
<n< ,
,∴当n<
 或n>
或n> 时,an>0;当
时,an>0;当  <n<
<n< 时,an<0,
时,an<0,∵f(n)=(2n-7)(3n-19)=6n2-59n+133
∴当n=
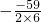 =
=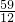 时,f(n)有最小值,且在(
时,f(n)有最小值,且在(  ,
, )上递减
)上递减∵
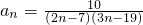 ,并且n∈N+,
,并且n∈N+,∴当n=3时,an有最大值为a3=
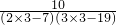 =1,
=1,当n=6时,an有最小值为a6=
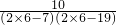 =-2,
=-2,∴该数列的最大项和最小项的和为-1.
故选D.
点评:本题是以函数的角度来求数列中的最大项和最小项问题,一定要注意各项的符号;构造关于n的二次函数,利用函数的单调性来求,但是n只取正整数.

练习册系列答案
相关题目
已知数列{an}的通项为an=2n-1,Sn为数列{an}的前n项和,令bn=
,则数列{bn}的前n项和的取值范围为( )
| 1 |
| Sn+n |
A、[
| ||||
B、(
| ||||
C、[
| ||||
D、[
|