题目内容
设 是奇函数,且在
是奇函数,且在 内是增函数,又
内是增函数,又 ,则
,则 的解集是 ( )
的解集是 ( )
A. B.
B.
C. D.
D.
【答案】
A
【解析】
试题分析:由 对x>1或x<1进行讨论,把不等式
对x>1或x<1进行讨论,把不等式 转化为f(x)>0或f(x)<0的问题解决,根据f(x)是奇函数,且在(0,+∞)内是增函数,又f(-3)=0,把函数值不等式转化为自变量不等式,求得结果.解;∵f(x)是奇函数,f(-3)=0,且在(0,+∞)内是增函数,∴f(3)=0,且在(-∞,0)内是增函数,∵
转化为f(x)>0或f(x)<0的问题解决,根据f(x)是奇函数,且在(0,+∞)内是增函数,又f(-3)=0,把函数值不等式转化为自变量不等式,求得结果.解;∵f(x)是奇函数,f(-3)=0,且在(0,+∞)内是增函数,∴f(3)=0,且在(-∞,0)内是增函数,∵ ,∴1°当x>1时,f(x)<0=f(3)∴1<x<3;2°当x<0时,f(x)>0=f(-3)∴-3<x<0. 3°当x=1时,不等式的解集为?.综上,
,∴1°当x>1时,f(x)<0=f(3)∴1<x<3;2°当x<0时,f(x)>0=f(-3)∴-3<x<0. 3°当x=1时,不等式的解集为?.综上, 的解集是{x|1<x<3或-3<x<0},故选A.
的解集是{x|1<x<3或-3<x<0},故选A.
考点:奇偶性和单调性
点评:考查函数的奇偶性和单调性解不等式,体现了分类讨论的思想方法,属基础题.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
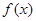 是奇函数,且在
是奇函数,且在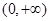 内是增函数,又
内是增函数,又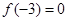 ,则
,则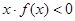 的解集是 ( )。
的解集是 ( )。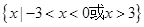 B.
B.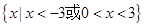
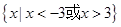 D.
D.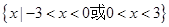
 是奇函数,且在
是奇函数,且在 内是增函数,又
内是增函数,又 ,则
,则 的解集是
的解集是  是奇函数,且在
是奇函数,且在 内是增函数,又
内是增函数,又 ,则
,则 的解集是( )
的解集是( ) B.
B.
 D.
D.