题目内容
设
，
，下列关系式成立的是（ ）A．a＞b
B．a+b＜1
C．a＜b
D．a+b=1
【答案】分析：利用微积分基本定理分别求出a、b，再利用三角函数的有关性质即可得出答案．
解答：解：∵（sinx）′=cosx，∴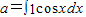
=
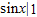=sin1；
∵（-cosx）′=sinx，∴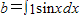
=
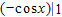=1-cos1．
∵sin1+cos1＞1，∴sin1＞1-cos1，即a＞b．
故选A．
点评：正确应用微积分基本定理和sin1+cos1＞1是解题的关键．
解答：解：∵（sinx）′=cosx，∴
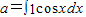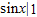==sin1；∵（-cosx）′=sinx，∴
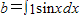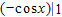==1-cos1．∵sin1+cos1＞1，∴sin1＞1-cos1，即a＞b．
故选A．
点评：正确应用微积分基本定理和sin1+cos1＞1是解题的关键．
练习册系列答案
相关题目
，
，下列关系式成立的是（ ）
，
，下列关系式成立的是（ ）
，
，下列关系式成立的是（ ）
，
，下列关系式成立的是（ ）