Question

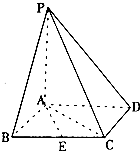（2012•广元三模）如图，四棱锥P-ABCD中，底面ABCD是梯形，AD∥BC，且AD=

3

4

BC，AB⊥AC，AB=AC=2，PA⊥平面ABCD，且E是BC中点，四面体P-BCA的体积为

8

3

．
（I）求异面直线AE与PC所成角的余弦值；
（Ⅱ）求点D到平面PBA的距离；
（Ⅲ）棱PC上是否存在点F，使DF⊥AC？若存在，求

PF

FC

的值；若不存在，说明理由．

Answer 1

分析：（I）以AB为x轴，以AC为y轴，以AP为z轴，建立空间直角坐标系，由题设知

AE

=(1，1，0)，

PC

=(0，2，-4)，由此能求出异面直线AE与PC所成角的余弦值．
（Ⅱ）由底面ABCD是梯形，AD∥BC，且AD=

3

4

BC，AB⊥AC，AB=AC=2，知D(-

3

2

，

3

2

，0)，故

AD

=(-

3

2

，

3

2

，0)，由平面PBA的法向量

n

=

AC

=(0，2，0)，能求出点D到平面PBA的距离．
（Ⅲ）设棱PC上是存在点F，使DF⊥AC时

PF

PC

=t，由

PC

=(0，2，-4)，知

PF

=(0，2t，-4t)，由此能导出棱PC上是存在点F，使DF⊥AC，此时

PF

FC

=3．

解答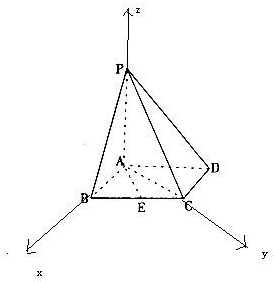：解：（I）以AB为x轴，以AC为y轴，以AP为z轴，建立空间直角坐标系，
∵四棱锥P-ABCD中，AB=AC=2，PA⊥平面ABCD，E是BC中点，
∴E（1，1，0），C（0，2，0），
∵四面体P-BCA的体积为

8

3

，
∴

1

3

×

1

2

×2×2×AP=

8

3

，∴AP=4，∴P（0，0，4），
∴

AE

=(1，1，0)，

PC

=(0，2，-4)，
设异面直线AE与PC所成角为α，
则cosα=|cos＜

AE

，

PC

＞|=|

AE • PC

| AE |•| PC  |

|=|

0+2+0

2 × 4+16

|=

10

10

．
（Ⅱ）∵底面ABCD是梯形，AD∥BC，且AD=

3

4

BC，AB⊥AC，AB=AC=2，
∴BC=

4+4

=2

2

，AD=

3

4

×2

2

=

3 2

2

，
∴D(-

3

2

，

3

2

，0)，∴

AD

=(-

3

2

，

3

2

，0)，
∵平面PBA的法向量

n

=

AC

=(0，2，0)，
∴点D到平面PBA的距离d=

| n • AD |

| n |

=

|0+3+0|

2

=

3

2

．
（Ⅲ）设棱PC上是存在点F，使DF⊥AC时

PF

PC

=t，
∵

PC

=(0，2，-4)，∴

PF

=(0，2t，-4t)，
∴

DF

=

DP

+

PF

=（

3

2

，-

3

2

，4）+（0，2t，-4t）=（

3

2

，2t-

3

2

，4-4t），
∵

AC

=(0，2，0)，

DF

⊥

AC

，
∴0+4t-3+0=0，t=

3

4

，
∴

PF

FC

=3．
故棱PC上是存在点F，使DF⊥AC，此时

PF

FC

=3．

点评：本题考查异面直线所成角的余弦值的求法，点到平面的距离的计算，探索线段上点的存在性．综合性强，难度大，有一定的探索性，是高考的重点．解题时要认真审题，仔细解答，注意向量法的合理运用．