题目内容
已知点A(cosx,1+cos2x),B(﹣λ+ sinx,cosx),x∈(0,π),向量
sinx,cosx),x∈(0,π),向量 =(1,0).
=(1,0).
(1)若向量 与
与 共线,求实数x的值;
共线,求实数x的值;
(2)若向量 ,求实数λ的取值范围.
,求实数λ的取值范围.
 sinx,cosx),x∈(0,π),向量
sinx,cosx),x∈(0,π),向量 =(1,0).
=(1,0).(1)若向量
 与
与 共线,求实数x的值;
共线,求实数x的值;(2)若向量
 ,求实数λ的取值范围.
,求实数λ的取值范围.解:(I)∵A(cosx,1+cos2x),B(﹣λ+ sinx,cosx),x∈(0,π),
sinx,cosx),x∈(0,π),
∴ ,
,
∵ =(1,0),向量
=(1,0),向量 与
与 共线,
共线,
∴1+cos2x﹣cosx=0,即2cos2x﹣cosx=0,
∴cosx=0,或cosx= .
.
又∵x∈(0,π),
∴x= 或x=
或x= .
.
(II)∵ ,
,
∴λ= =2sin(x﹣
=2sin(x﹣ ),
),
∵0<x<π,
∴﹣ ,
,
∴﹣ ,
,
∴﹣1<λ≤2,
∴λ的取值范围是(﹣1,2].
 sinx,cosx),x∈(0,π),
sinx,cosx),x∈(0,π),∴
 ,
,∵
 =(1,0),向量
=(1,0),向量 与
与 共线,
共线,∴1+cos2x﹣cosx=0,即2cos2x﹣cosx=0,
∴cosx=0,或cosx=
 .
.又∵x∈(0,π),
∴x=
 或x=
或x= .
.(II)∵
 ,
,∴λ=
 =2sin(x﹣
=2sin(x﹣ ),
),∵0<x<π,
∴﹣
 ,
,∴﹣
 ,
,∴﹣1<λ≤2,
∴λ的取值范围是(﹣1,2].

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
 sinx,cosx),x∈(0,π),向量
sinx,cosx),x∈(0,π),向量 =(1,0).
=(1,0). 与
与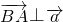 ,求实数λ的取值范围.
,求实数λ的取值范围. sinx,cosx),x∈(0,π),向量
sinx,cosx),x∈(0,π),向量 =(1,0).
=(1,0).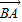 与
与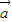 共线,求实数x的值;
共线,求实数x的值;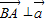 ,求实数λ的取值范围.
,求实数λ的取值范围.