题目内容
△ABC中,己知∠A>∠B>∠C,且∠A=2∠C,b=4,a+c=8,求a,c的长.
a= ,c=
,c= .
.
 ,c=
,c= .
.本试题考查了解三角形的运用。
解:由正弦定理 =
=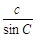 及∠A=2∠C,得
及∠A=2∠C,得
 =
=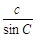 ,即
,即 =
=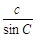 ,
,
∴cos C= . …………3分
. …………3分
由余弦定理cos C=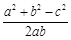 ,
,
∵b=4,a+c=8,
∴a+c=2b,
∴cos C= =
= =
=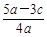 ,
,
∴ =
=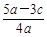 , …………9分
, …………9分
整理得(2a-3c)(a-c)=0,
∵a≠c,∴2a=3c.
又∵a+c=8,
∴a= ,c=
,c= . …………15分
. …………15分
另解:由正弦定理 =
=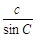 及∠A=2∠C,得
及∠A=2∠C,得
 =
=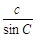 ,即
,即 =
=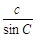 ,
,
∴cos C= . …………3分
. …………3分
又因
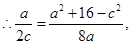 …………9分
…………9分
即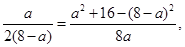
 解之得
解之得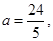 或
或
 时要舍去,
时要舍去, 此时
此时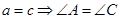 与∠A=2∠C矛盾,
与∠A=2∠C矛盾,
由此可得a= ,c=
,c= . …………15分
. …………15分
解:由正弦定理
 =
=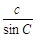 及∠A=2∠C,得
及∠A=2∠C,得 =
=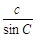 ,即
,即 =
=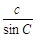 ,
,∴cos C=
 . …………3分
. …………3分由余弦定理cos C=
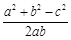 ,
,∵b=4,a+c=8,
∴a+c=2b,
∴cos C=
 =
= =
=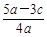 ,
, ∴
 =
=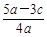 , …………9分
, …………9分整理得(2a-3c)(a-c)=0,
∵a≠c,∴2a=3c.
又∵a+c=8,
∴a=
 ,c=
,c= . …………15分
. …………15分另解:由正弦定理
 =
=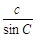 及∠A=2∠C,得
及∠A=2∠C,得 =
=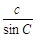 ,即
,即 =
=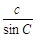 ,
,∴cos C=
 . …………3分
. …………3分又因

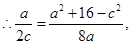 …………9分
…………9分即
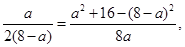
 解之得
解之得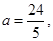 或
或
 时要舍去,
时要舍去, 此时
此时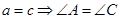 与∠A=2∠C矛盾,
与∠A=2∠C矛盾,由此可得a=
 ,c=
,c= . …………15分
. …………15分
练习册系列答案
相关题目
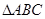 中,内角A、B、C的对边长分别为
中,内角A、B、C的对边长分别为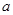 、
、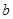 、
、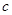 ,已知
,已知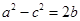 ,且
,且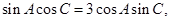 则b=____________.
则b=____________. ,其中有两解的是
,其中有两解的是
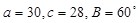
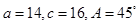
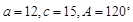
 ,求边长a , b ;(2).若
,求边长a , b ;(2).若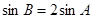 ,求ΔABC的面积.
,求ΔABC的面积.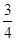 ,求b的值
,求b的值
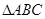 中,
中,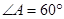 ,
,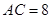 ,面积
,面积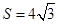 ,则
,则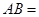
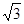
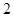
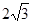

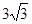
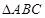 中,角
中,角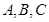 所对的边分别是
所对的边分别是 ,若
,若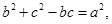 且
且 则角
则角 = ;
= ; 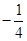 .
.