Question

已知函数f（x）=ax﹣1﹣lnx（a∈R）

（1）讨论函数f（x）的单调性；

（2）若函数f（x）在x=1处取得极值，不等式f（x）≥bx﹣2对∀x∈（0，+∞）恒成立，求实数b的取值范围；

（3）当x＞y＞e﹣1时，证明不等式e^xln（1+y）＞e^yln（1+x）

Answer 1

考点：

利用导数研究函数的单调性；函数在某点取得极值的条件；导数在最大值、最小值问题中的应用．

专题：

计算题；综合题；函数的性质及应用；导数的综合应用．

分析：

（1）由f（x）=ax﹣1﹣lnx，求得f′（x）=．然后分a≤0与a＞0两种情况讨论，从而得到f′（x）的符号，可得f（x）在其定义域（0，+∞）内的单调性，最后综合可得答案；

（2）函数f（x）在x=1处取得极值，由（1）的讨论可得a=1．将不等式f（x）≥bx﹣2化简整理得到1+﹣≥b，再构造函数g（x）=1+﹣，利用导数研究g（x）的单调性，得到[g（x）]_min=1﹣]．由此即可得到实数b的取值范围；

（3）设函数F（t）=，其中t＞e﹣1．利用导数研究F（x）的单调性，得到得F（t）是（e﹣1，+∞）上的增函数．从而得到当x＞y＞e﹣1时，F（x）＞F（y）即＞，变形整理即可得到不等式e^xln（1+y）＞e^yln（1+x）成立．

解答：

解：（1）∵f（x）=ax﹣1﹣lnx，∴f′（x）=a﹣=，

当a≤0时，f'（x）≤0在（0，+∞）上恒成立，

∴函数f（x）在（0，+∞）单调递减；

当a＞0时，f'（x）＜0得 0＜x≤，f'（x）＞0得x＞，

∴f（x）在（0，）上单调递减，在（，+∞）上单调递增，

综上所述，当a≤0时函数f（x）在（0，+∞）上是减函数；

当a＞0时，f（x）在（0，）上是减函数，在（，+∞）上是增函数．

（2）∵函数f（x）在x=1处取得极值，∴根据（1）的结论，可得a=1，

∴f（x）≥bx﹣2，即x+1﹣lnx≥bx，两边都除以正数x，得1+﹣≥b，

令g（x）=1+﹣，则g′（x）=﹣﹣=﹣（2﹣lnx），

由g′（x）＞0得，x＞e²，∴g（x）在（0，e²）上递减，

由g′（x）＜0得，0＜x＜e²，∴g（x）在（e²，+∞）上递增，

∴g（x）_min=g（e²）=1﹣，

可得b≤1﹣，实数b的取值范围为（﹣∞，1﹣]．

（3）令F（t）=，其中t＞e﹣1

可得F'（t）==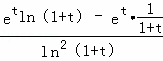

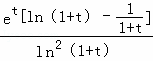
再设G（t）=ln（1+t）﹣，可得G'（t）=+＞0在（e﹣1，+∞）上恒成立

∴G（t）是（e﹣1，+∞）上的增函数，可得G（t）＞G（e﹣1）=lne﹣=1﹣＞0

因此，F'（t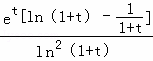）=＞0在（e﹣1，+∞）上恒成立，可得F（t）=是（e﹣1，+∞）上的增函数．

∵x＞y＞e﹣1，∴F（x）＞F（y），可得＞

∵ln（1+x）＞0且ln（1+y）＞0，∴不等式两边都乘以ln（1+x）ln（1+y），可得e^xln（1+y）＞e^yln（1+x）．

即对任意x＞y＞e﹣1，都有不等式e^xln（1+y）＞e^yln（1+x）成立．

点评：

本题考查利用导数研究函数的极值，考查恒成立问题，着重考查分类讨论思想与构造函数思想的应用，体现综合分析问题与解决问题能力，属于难题．