题目内容
(本小题满分12分)
已知函数![]()
(1)若函数![]() 在[1,2]上是减函数,求实数a的取值范围;
在[1,2]上是减函数,求实数a的取值范围;
(2)令![]() ,是否存在实数a,当
,是否存在实数a,当![]() (e是自然常数)时,函数
(e是自然常数)时,函数![]() 的最小值是3,若存在,求出a的值;若不存在,说明理由。
的最小值是3,若存在,求出a的值;若不存在,说明理由。
解:(1)因为函数f(x)在[1,2]上是减函数,所以:
![]() 在[1,2]上恒成立
在[1,2]上恒成立
令![]() ,有
,有![]() 得
得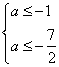 得
得![]() -----------------5分
-----------------5分
(2)假设存在实数a,使![]() 有最小值3,
有最小值3,![]()
①当![]() 时,
时,![]() ,所以
,所以
![]() 在(0,e]上单调递减,
在(0,e]上单调递减,![]() (舍去)
(舍去)
②当![]() 时,
时,![]() 在(0,e]上恒成立
在(0,e]上恒成立
所以![]() 在(0,e]上单调递减,
在(0,e]上单调递减,![]() (舍去)
(舍去)
③当![]() 时,令
时,令![]() 所以
所以![]() 在
在![]() 上递减
上递减
在![]() 上递增
上递增![]()
![]() 满足条件 综上,存在
满足条件 综上,存在![]() 使
使![]() 时
时![]() 有最小值3--------------13分
有最小值3--------------13分

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目