Question

函数f（x）=e^x（x²-2x）的单调递减区间为________．

Answer 1

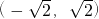
分析：求导，[e^x（x²-2x）]′=（e^x）′（x²-2x）+e^x（x²-2x）′，（e^x）′=e^x，令导数小于0，得x的取值区间，即为f（x）的单调减区间．
解答：f′（x）=e^x（x²-2x）+e^x（2x-2）=e^x（x²-2），
令f′（x）＜0得-＜x＜，
∴函数f（x）的单调递减区间为（-，）．
故答案为：（-，）．
点评：考查利用导数求函数的单调区间，令f′（x）＜0，得x的取值区间，即为f（x）的单调减区间．是基础题．