题目内容
5.设f(x)=xex(e为自然对数的底数),g(x)=(x+1)2.(I)记$F(x)=\frac{f(x)}{g(x)}$.
(i)讨论函数F(x)单调性;
(ii)证明当m>0时,F(-1+m)>F(-1-m)恒成立;
(II)令G(x)=af(x)+g(x)(a∈R),设函数G(x)有两个零点,求参数a的取值范围.
分析 (Ⅰ)(i)求出F(x0的导数,由导数大于0,可得增区间;导数小于0,可得减区间;
(ii)作差可得F(-1+m)-F(-1-m),令φ(m)=$\frac{m-1}{m+1}$e2m+1,求出导数,判断单调性即可得证;
(Ⅱ)由已知,求得G(x)的导数,讨论a=0,a>0,a<0,运用单调性,求出G(x)的极小值,结合函数的零点个数,即可得到所求a的范围.
解答 解:(Ⅰ)$F(x)=\frac{f(x)}{g(x)}$=$\frac{x{e}^{x}}{(x+1)^{2}}$(x≠-1),
(i)F′(x)=$\frac{(x+1){e}^{x}•(x+1)^{2}-x{e}^{x}•2(x+1)}{(x+1)^{4}}$=$\frac{{e}^{x}•({x}^{2}+1)}{(x+1)^{3}}$,…(2分)
所以,当x∈(-∞,-1)时,F′(x)<0,F(x)单调减;
当x∈(-1,+∞)时,F′(x)<0,F(x)单调增; …(3分)
(ii)F(-1+m)-F(-1-m)=$\frac{(m-1){e}^{m-1}}{{m}^{2}}$-$\frac{(-m-1){e}^{-m-1}}{{m}^{2}}$=$\frac{m+1}{{m}^{2}{e}^{m+1}}$($\frac{m-1}{m+1}$e2m+1),
令φ(m)=$\frac{m-1}{m+1}$e2m+1=e2m-$\frac{2{e}^{2m}}{m+1}$+1(m>0),
φ′(m)=2e2m-$\frac{4{e}^{2m}(m+1)-2{e}^{2m}}{(m+1)^{2}}$=$\frac{2{m}^{2}{e}^{2m}}{(m+1)^{2}}$>0,…(5分)
所以φ(m)在m>0递增,即有φ(m)>φ(0)=0,又$\frac{m+1}{{m}^{2}{e}^{m+1}}$>0,
所以m>0时,F(-1+m)-F(-1-m)=$\frac{m+1}{{m}^{2}{e}^{m+1}}$($\frac{m-1}{m+1}$e2m+1)>0恒成立,即
当m>0时,F(-1+m)>F(-1-m)恒成立. …(6分)
(Ⅱ)由已知,G(x)=af(x)+g(x)=axex+(x+1)2,
G′(x)=a(x+1)ex+2(x+1)=(x+1)(aex+2).
①当a=0时,G(x)=(x+1)2,有唯一零点-1; …(7分)
②当a>0时,aex+2>0,所以
当x<-1时,G′(x)<0,G(x)单调减;
当x>-1时,G′(x)>0,G(x)单调增.
所以G(x)极小值为G(-1)=-$\frac{a}{e}$<0,
因G(0)=1>0,所以当x>-1时,G(x)有唯一零点;
当x<-1时,ax<0,ex<$\frac{1}{e}$,所以axex>$\frac{ax}{e}$,
所以G(x)>>$\frac{ax}{e}$+(x+1)2=x2+(2+$\frac{a}{e}$)x+1,
因为(2+$\frac{a}{e}$)2-4×1×1=$\frac{4a}{e}$+($\frac{a}{e}$)2>0,
所以,?t1,t2,且t1<t2,当x<t1,或x>t2时,使x2+(2+$\frac{a}{e}$)x+1>0,
取x0∈(-∞,-1)∪(-∞,t1),则G(x0)>0,从而可知
当x<-1时,G(x)有唯一零点,
即当a>0时,函数G(x)有两个零点. …(10分)
③当a<0时,G′(x)=a(x+1)(ex-(-$\frac{2}{a}$)),由G′(x)=0,得x=-1,或x=ln(-$\frac{2}{a}$).
(1)若-1=ln(-$\frac{2}{a}$),即a=-2e时,G′(x)=-2e(x+1)(ex-$\frac{1}{e}$)≤0,
所以G(x)是单调减函数,至多有一个零点;
(2)若-1>ln(-$\frac{2}{a}$),即a<-2e时,G′(x)=a(x+1)(ex-(-$\frac{2}{a}$)),
注意到y=x+1,y=ex+$\frac{2}{a}$,都是增函数,
所以,当x<ln(-$\frac{2}{a}$)时,G′(x)<0,G(x)是单调减函数;
当ln(-$\frac{2}{a}$)<x<-1时,G′(x)>0,G(x)是单调增函数;
当x>-1时,G′(x)<0,G(x)是单调减函数.
G(x)的极小值为G(ln(-$\frac{2}{a}$))=aln(-$\frac{2}{a}$)•(-$\frac{2}{a}$)+(ln(-$\frac{2}{a}$)+1)2=ln2(-$\frac{2}{a}$)+1>0,
所以G(x)至多有一个零点; …(12分)
(3)若-1<ln(-$\frac{2}{a}$),即0>a>-2e时,同理可得
当x<-1时,G′(x)<0,G(x)是单调减函数;
当-1<x<ln(-$\frac{2}{a}$)时,G′(x)>0,G(x)是单调增函数;
当x>ln(-$\frac{2}{a}$)时,G′(x)<0,G(x)是单调减函数.
所以G(x)的极小值为G(-1)=-$\frac{a}{e}$<0,G(x)至多有一个零点.
综上,若函数G(x)有两个零点,则参数a的取值范围是(0,+∞).…(14分)
点评 本题考查函数的单调性的判断,注意运用导数,考查不等式恒成立问题的解法,注意运用导数判断单调性,运用作差法和构造函数法,同时考查函数零点问题,注意运用分类讨论和转化思想,属于难题.

| A. | $\frac{\sqrt{3}}{3}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{2}$ |
| A. | 8 | B. | 8$\sqrt{2}$ | C. | 16 | D. | 16$\sqrt{2}$ |
| A. | (x-1)2+(y-$\sqrt{2}$)2=2 | B. | (x-1)2+(y-2)2=2 | C. | (x+1)2+(y+$\sqrt{2}$)2=4 | D. | (x-1)2+(y-$\sqrt{2}$)2=4 |
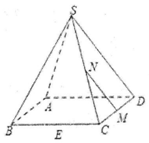 如图,在正四棱锥S-ABCD中,E.M.N分别是BC.CD.SC的中点,动点P的线段MN上运动时,下列四个结论:
如图,在正四棱锥S-ABCD中,E.M.N分别是BC.CD.SC的中点,动点P的线段MN上运动时,下列四个结论: