题目内容
已知 的展开式中第3项的系数与第5项的系数之比为
的展开式中第3项的系数与第5项的系数之比为 .
.(1)求n的值;
(2)求展开式中的常数项.
【答案】分析:(1)直接根据 的展开式中第3项的系数与第5项的系数之比为
的展开式中第3项的系数与第5项的系数之比为 列出关于n的方程,结合组合数的性质即可求出结论;
列出关于n的方程,结合组合数的性质即可求出结论;
(2)先求出其通项,再令自变量的指数为0即可求出结论.
解答:解:(1)由题设,得 ,
,
则
 ⇒n2-5n-50=0⇒n=10或n=-5(舍)
⇒n2-5n-50=0⇒n=10或n=-5(舍)
(2) =
=
当
即当r=8时为常数项 .
.
点评:本题主要考查二项式定理以及组合数的应用.一般在求解二次式定理方面的题目时,求特定项属于必考题目.
 的展开式中第3项的系数与第5项的系数之比为
的展开式中第3项的系数与第5项的系数之比为 列出关于n的方程,结合组合数的性质即可求出结论;
列出关于n的方程,结合组合数的性质即可求出结论;(2)先求出其通项,再令自变量的指数为0即可求出结论.
解答:解:(1)由题设,得
 ,
,则

 ⇒n2-5n-50=0⇒n=10或n=-5(舍)
⇒n2-5n-50=0⇒n=10或n=-5(舍)(2)
 =
=
当

即当r=8时为常数项
 .
.点评:本题主要考查二项式定理以及组合数的应用.一般在求解二次式定理方面的题目时,求特定项属于必考题目.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目
 的展开式中第3项与第5项的系数之比为
的展开式中第3项与第5项的系数之比为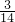 .
. 的展开式中第3项的系数与第5项的系数之比为
的展开式中第3项的系数与第5项的系数之比为 。
。 的展开式中第3项与第5项的系数之比为
的展开式中第3项与第5项的系数之比为 .
. 的展开式中第3项的系数与第5项的系数之比为
的展开式中第3项的系数与第5项的系数之比为 .
. 的值;(2)求展开式中的常数项.
的值;(2)求展开式中的常数项.