Question

已知函数f（x）=ln（x+）-x²-x在x = 0处取得极值．

（1）求实数的值；

（2）若关于x的方程，f（x）= 在区间[0，2]上恰有两个不同的实数根，求实数的取值范围；

（3）证明：对任意的正整数n，不等式都成立．

Answer 1

       解：（1）  =  ∵x=0时，f（x）取得极值，∴=0，

       故 =0，解得a=1．经检验a=1符合题意．

       （2）由a=1知f（x）=ln（x+1）-x² - x，由f（x）= ,得ln（x+1）-x²+ x-b=0，

       令φ（x）= ln（x+1）-x²+ x-b，则f（x）= +b在[0，2]上恰有两个不同的实数根等价于φ（x）=0在[0，2]恰有两个不同实数根．，

       当x∈（0，1）时， >O，于是φ（x）在（0，1）上单调递增；

       当x∈（1，2）时， <0，于是φ（x）在（1，2）上单调递减．

       依题意有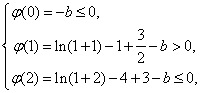 ∴ln3 -1≤b<ln2 +

（Ⅲ） f（x）=ln（x+1）-x² –x的定义域为{x|x> -1}，由（Ⅰ）知，

令=0得，x=0或x= -（舍去）， ∴当-1<x<0时，>0，f（x）单调递增；

当x>0时，<0，f（x）单调递减．∴f（0）为f（x）在（-1,+∞）上的最大值．

∴f（x）≤ f（0），故ln（x+1）-x²-x≤0（当且仅当x=0时，等号成立）．

对任意正整数n，取x=>0得，ln（+1）< +，故ln（）<．

 

则

即，当时上式也成立，因此

对任意的正整数n，不等式都成立