Question

如图：先将等腰Rt△ABC的斜边与有一个角为30°的Rt△ADB的斜边重合，然后将等腰Rt△ABC沿着斜边AB翻折成三棱锥C-ABD，若AB=2，则V_C-ABD的最大值为

3

6

．

Answer 1

分析：根据棱锥的体积公式，在底面积不变的情况下，体积的大小取决于高，当平面ABD⊥平面ABC时，高最大，求出即可．

解答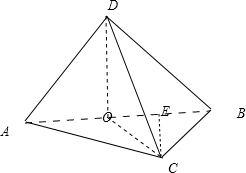：解：过D作DO⊥AB，交AB于O，
∵棱锥的体积公式，在底面积不变的情况下，体积的大小取决于高，
∴当DO⊥平面ABC时，棱锥的高最大，
AB=2，DO=1，BC=1，AC=AB×cos30°=

3

，
此时V_棱锥=

1

3

×

1

2

×AC×BC×DO=

1

6

×

3

×1×1=

3

6

．
故答案是

3

6

．

点评：本题考查面面垂直的性质，考查三棱锥体积的计算．