题目内容
在平面直角坐标系xoy中,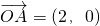 ,点C为圆(x+2)2+(y-2)2=2上的动点,则
,点C为圆(x+2)2+(y-2)2=2上的动点,则 与
与 夹角的取值范围是________.
夹角的取值范围是________.
[ π,
π, π]
π]
分析:如图,OM,ON为圆P(x+2)2+(y-2)2=2的两条切线.可知当C与M重合时, 与
与 夹角最小,当C与N重合时,
夹角最小,当C与N重合时, 与
与 夹角最大.
夹角最大.
解答: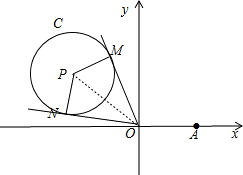 解:如图,OM,ON为圆P(x+2)2+(y-2)2=2的两条切线.可知当C与M重合时,
解:如图,OM,ON为圆P(x+2)2+(y-2)2=2的两条切线.可知当C与M重合时, 与
与 夹角最小,
夹角最小,
此时在RT△OMP中,OP=2 ,PM=r=
,PM=r= ,
,
所以∠POM=30°,∠MOy=∠POy-∠POM=45°-30°=15°, 与
与 夹角∠MOA=90°+15°=105°=
夹角∠MOA=90°+15°=105°= .
.
当C与N重合时, 与
与 夹角最大,此时∠NOA=180°-15°=165°=
夹角最大,此时∠NOA=180°-15°=165°= .
.
 与
与 夹角的取值范围是[
夹角的取值范围是[ ,
, ].
].
故答案为:[ ,
, ].
].
点评:本题考查向量夹角的计算,解题方法采用了数形结合的思想方法.用到了圆的切线的性质.
 π,
π, π]
π]分析:如图,OM,ON为圆P(x+2)2+(y-2)2=2的两条切线.可知当C与M重合时,
 与
与 夹角最小,当C与N重合时,
夹角最小,当C与N重合时, 与
与 夹角最大.
夹角最大.解答:
 解:如图,OM,ON为圆P(x+2)2+(y-2)2=2的两条切线.可知当C与M重合时,
解:如图,OM,ON为圆P(x+2)2+(y-2)2=2的两条切线.可知当C与M重合时, 与
与 夹角最小,
夹角最小,此时在RT△OMP中,OP=2
 ,PM=r=
,PM=r= ,
,所以∠POM=30°,∠MOy=∠POy-∠POM=45°-30°=15°,
 与
与 夹角∠MOA=90°+15°=105°=
夹角∠MOA=90°+15°=105°= .
.当C与N重合时,
 与
与 夹角最大,此时∠NOA=180°-15°=165°=
夹角最大,此时∠NOA=180°-15°=165°= .
. 与
与 夹角的取值范围是[
夹角的取值范围是[ ,
, ].
].故答案为:[
 ,
, ].
].点评:本题考查向量夹角的计算,解题方法采用了数形结合的思想方法.用到了圆的切线的性质.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
在平面直角坐标系xOy中,双曲线中心在原点,焦点在y轴上,一条渐近线方程为x-2y=0,则它的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.