题目内容
某车站每天上午发出两班客车,第一班客车在8:00,8:20,8:40这三个时刻随机发出,且在8:00发出的概率为| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
(1)请预测旅客乘到第一班客车的概率;
(2)旅客候车时间的分布列;
(3)旅客候车时间的数学期望.
分析:(1)第一班若在8:20或8:40发出,则旅客能乘到,这两个事件是互斥的,根据互斥事件的概率公式得到其概率.
(2)由题意知候车时间X的可能取值是10,30,50,70,90,根据条件中所给的各个事件的概率,和两班客车发出时刻是相互独立的,得到各个变量对应的概率,写出分布列.
(3)根据上一问做出的分布列,代入求概率的公式,求出随机变量的期望值,得到旅客候车时间的数学期望.
(2)由题意知候车时间X的可能取值是10,30,50,70,90,根据条件中所给的各个事件的概率,和两班客车发出时刻是相互独立的,得到各个变量对应的概率,写出分布列.
(3)根据上一问做出的分布列,代入求概率的公式,求出随机变量的期望值,得到旅客候车时间的数学期望.
解答:解:(1)∵在8:00发出的概率为
,8:20发出的概率为
,
第一班若在8:20或8:40发出,则旅客能乘到,这两个事件是互斥的,
根据互斥事件的概率公式得到其概率为P=
+
=
.
(2)由题意知候车时间X的可能取值是10,30,50,70,90
根据条件中所给的各个事件的概率,得到
P(X=10)=
,P(X=30)=
,P(X=50)=
×
=
,
P(X=70)=
×
=
,P(X=90)=
,
∴旅客候车时间的分布列为:
(3)候车时间的数学期望为
10×
+30×
+50×
+70×
+90×
=5+
+
+
+
=30.
即这旅客候车时间的数学期望是30分钟.
| 1 |
| 4 |
| 1 |
| 2 |
第一班若在8:20或8:40发出,则旅客能乘到,这两个事件是互斥的,
根据互斥事件的概率公式得到其概率为P=
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
(2)由题意知候车时间X的可能取值是10,30,50,70,90
根据条件中所给的各个事件的概率,得到
P(X=10)=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 16 |
P(X=70)=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 16 |
∴旅客候车时间的分布列为:
| 候车时间X(分) | 10 | 30 | 50 | 70 | 90 | ||||||||||
| 概率 |
|
|
|
|
|
10×
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 16 |
| 1 |
| 8 |
| 1 |
| 16 |
=5+
| 15 |
| 2 |
| 25 |
| 8 |
| 35 |
| 4 |
| 45 |
| 8 |
即这旅客候车时间的数学期望是30分钟.
点评:本题考查互斥事件的概率公式,考查离散型随机变量的分布列和期望值,考查相互独立事件同时发生的概率,本题是一个概率与统计的综合题目,是一个可以出现在高考卷中的题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
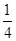 ,8∶20发出的概率为
,8∶20发出的概率为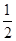 ,8∶40发出的概率为
,8∶40发出的概率为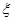 的分布列和数学期望。
的分布列和数学期望。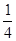 ,8∶20发出的概率为
,8∶20发出的概率为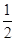 ,8∶40发出的概率为
,8∶40发出的概率为