题目内容
已知双曲线的方程是x2 - 4y2 = 4,则此双曲线的离心率为( )
A. | B. | C. | D. |
D
解析

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设点 是椭圆
是椭圆 上一动点,
上一动点, 是椭圆的两个焦点,
是椭圆的两个焦点, 的内切圆半径为
的内切圆半径为 ,则当点点
,则当点点 在
在 轴上方时,点
轴上方时,点 的纵坐标为( )
的纵坐标为( )
| A.2 | B.4 | C.  | D. |
在 中,
中, ,
, .若以
.若以 为焦点的椭圆经过点
为焦点的椭圆经过点 ,则该椭圆的离心率为( )
,则该椭圆的离心率为( )
A. | B. | C. | D.2 |
过点F(0,3),且和直线 相切的动圆圆心轨迹方程是( )
相切的动圆圆心轨迹方程是( )
A. | B. | C. | D. |
若抛物线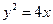 的焦点是
的焦点是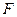 ,准线是
,准线是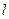 ,点
,点 是抛物线上一点,则经过点
是抛物线上一点,则经过点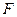 、
、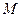 且与
且与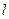 相切的圆共有 ( ).
相切的圆共有 ( ).
A.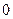 个 个 | B. 个 个 | C.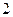 个 个 | D.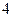 个 个 |
若抛物线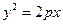 的焦点与椭圆
的焦点与椭圆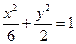 的右焦点重合,则
的右焦点重合,则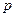 的值为( ﹡ )
的值为( ﹡ )
A.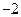 | B. | C. | D.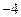 |
(10)设O为坐标原点,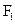 ,
,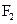 是双曲线
是双曲线 (a>0,b>0)的焦点,若在双曲线上存在点P,满足∠
(a>0,b>0)的焦点,若在双曲线上存在点P,满足∠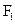 P
P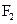 =60°,∣OP∣=
=60°,∣OP∣=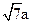 ,则该双曲线的渐近线方程为
,则该双曲线的渐近线方程为
A.x±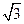 y="0" y="0" | B.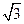 x±y=0 x±y=0 |
C.x±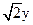 ="0" ="0" | D.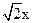 ±y=0 ±y=0 |
 =1的焦点为顶点,顶点为焦点的椭圆方程为 ( )
=1的焦点为顶点,顶点为焦点的椭圆方程为 ( ) B.
B.  C.
C.  D.
D. 是椭圆的两个焦点,过
是椭圆的两个焦点,过 且与椭圆长轴垂直的直线交椭圆于A、B两点,若
且与椭圆长轴垂直的直线交椭圆于A、B两点,若 是等腰直角三角形,则这个椭圆的离心率是
是等腰直角三角形,则这个椭圆的离心率是 B.
B.
 D.
D.