题目内容
已知函数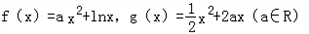 .
.
(1)若函数f(x)在x=1处取得极值,求函数f(x)的单调增区间;
(2)若f(x)<g(x)在区间(1,+∞)上恒成立,求实数a的取值范围.
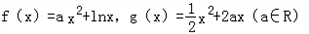 .
.(1)若函数f(x)在x=1处取得极值,求函数f(x)的单调增区间;
(2)若f(x)<g(x)在区间(1,+∞)上恒成立,求实数a的取值范围.
解:(1)求导函数,可得f′(x)=2ax+ (x∈(0,+∞))
(x∈(0,+∞))
∵函数f(x)在x=1处取得极值,
∴f′(x)=0,∴2a+1=0,
∴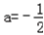 ∴f′(x)=﹣x+
∴f′(x)=﹣x+
令f′(x)>0,x>0可得0<x<1
∴函数f(x)的单调增区间为(0,1);
(2)构造函数F(x)=f(x)﹣g(x),
则F′(x)=f′(x)﹣g′(x)=2ax+ ﹣x﹣2a=
﹣x﹣2a=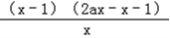
若a≥1,则x>1时,F′(x)>0,函数在(1,+∞)上单调增,F(x)<0不恒成立;
若 <a<1,则函数在(1,
<a<1,则函数在(1,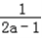 )上F′(x)<0,在(
)上F′(x)<0,在(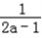 ,+∞)上F′(x)>0,
,+∞)上F′(x)>0,
∴F(x)<0不恒成立;
若a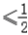 ,则x>1时,F′(x)<0,函数在(1,+∞)上单调减,
,则x>1时,F′(x)<0,函数在(1,+∞)上单调减,
故只需要F(1)≤0
∴a﹣ ﹣2a≤0
﹣2a≤0
∴a≥﹣
∴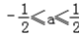
 (x∈(0,+∞))
(x∈(0,+∞))∵函数f(x)在x=1处取得极值,
∴f′(x)=0,∴2a+1=0,
∴
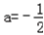 ∴f′(x)=﹣x+
∴f′(x)=﹣x+
令f′(x)>0,x>0可得0<x<1
∴函数f(x)的单调增区间为(0,1);
(2)构造函数F(x)=f(x)﹣g(x),
则F′(x)=f′(x)﹣g′(x)=2ax+
 ﹣x﹣2a=
﹣x﹣2a=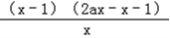
若a≥1,则x>1时,F′(x)>0,函数在(1,+∞)上单调增,F(x)<0不恒成立;
若
 <a<1,则函数在(1,
<a<1,则函数在(1,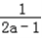 )上F′(x)<0,在(
)上F′(x)<0,在(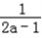 ,+∞)上F′(x)>0,
,+∞)上F′(x)>0,∴F(x)<0不恒成立;
若a
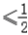 ,则x>1时,F′(x)<0,函数在(1,+∞)上单调减,
,则x>1时,F′(x)<0,函数在(1,+∞)上单调减,故只需要F(1)≤0
∴a﹣
 ﹣2a≤0
﹣2a≤0∴a≥﹣

∴
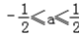

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目





 的定义域为
的定义域为 ,部分函数值如表所示,其导函数的图象如图所示,若正数
,部分函数值如表所示,其导函数的图象如图所示,若正数 ,
, 满足
满足 ,则
,则 的取值范围是( )
的取值范围是( ) 



 B.
B. C.
C. D.
D.
 ,如果满足;对任意
,如果满足;对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 ,
,
 时,求函数
时,求函数 上的值域,并判断函数
上的值域,并判断函数 上是以3为上界函数值,求实数
上是以3为上界函数值,求实数 的取值范围;
的取值范围; ,求函数
,求函数 在
在 上的上界T的取值范围。
上的上界T的取值范围。 ,如果满足;对任意
,如果满足;对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 ,
,
 时,求函数
时,求函数 上的值域,并判断函数
上的值域,并判断函数 上是以3为上界函数值,求实数
上是以3为上界函数值,求实数 的取值范围;
的取值范围; ,求函数
,求函数 在
在 上的上界T的取值范围。
上的上界T的取值范围。