题目内容
 (2012•唐山二模)已知某几何体的三视图如图所示,则其体积为( )
(2012•唐山二模)已知某几何体的三视图如图所示,则其体积为( )分析:由三视图可知若求该几何体的体积,可将该几何体分成三部分:两端体积相等的两个四棱锥,中间为直棱柱.分别求体积再相加.
解答: 解:由三视图可知,该几何体的直观图如图所示的多面体ABCDEF,
解:由三视图可知,该几何体的直观图如图所示的多面体ABCDEF,
将该几何体分成三部分:两端体积相等的两个四棱锥,中间为直棱柱.
两个四棱锥体积之和2V1=2×
×(2×0.5)×1=
直棱柱体积V2=
×2×1×1=1,
故所求体积为1+
=
故选C.
 解:由三视图可知,该几何体的直观图如图所示的多面体ABCDEF,
解:由三视图可知,该几何体的直观图如图所示的多面体ABCDEF,将该几何体分成三部分:两端体积相等的两个四棱锥,中间为直棱柱.
两个四棱锥体积之和2V1=2×
| 1 |
| 3 |
| 2 |
| 3 |
直棱柱体积V2=
| 1 |
| 2 |
故所求体积为1+
| 2 |
| 3 |
| 5 |
| 3 |
故选C.
点评:本题考查三视图求几何体的体积,考查计算能力,空间想象能力,三视图复原几何体是解题的关键

练习册系列答案
相关题目
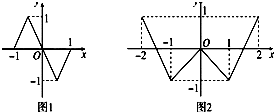 (2012•唐山二模)奇函数f(x)、偶函数g(x)的图象分别如图1、2所示,方程f(g(x))=0、g(f(x))=0的实根个数分别为a、b,则a+b=( )
(2012•唐山二模)奇函数f(x)、偶函数g(x)的图象分别如图1、2所示,方程f(g(x))=0、g(f(x))=0的实根个数分别为a、b,则a+b=( )