题目内容
已知α,β为锐角,若sinα=
,cos(α+β)=-
,试求cosβ的值.
| 4 |
| 5 |
| 3 |
| 5 |
分析:法1:通过α,β为锐角,若sinα=
,cos(α+β)=-
,求出cosα,利用两角和的余弦函数推出sinβ=
+
cosβ,通过同角三角函数的基本关系式,求出结果.
法2:求出cosα,利用cos(α+β)=-cosα=cos(π-α)而α,β为锐角,推出α+β=π-α,通过二倍角公式解答即可.
| 4 |
| 5 |
| 3 |
| 5 |
| 3 |
| 4 |
| 3 |
| 4 |
法2:求出cosα,利用cos(α+β)=-cosα=cos(π-α)而α,β为锐角,推出α+β=π-α,通过二倍角公式解答即可.
解答:解:法1:联立方程组求解:由α为锐角,sinα=
,得cosα=
所以:cos(α+β)=cosα×cosβ-sinα×sinβ=
cosβ-
sinβ=-
(1)
由(1)知sinβ=
+
cosβ再联立 sin2β+cos2β=1可得cosβ=-1或cosβ=
又β为锐角,所以cosβ=
解法2:由 α为锐角,sinα=
,得cosα=
,
此时cos(α+β)=-cosα=cos(π-α)而α,β为锐角,所以α+β=π-α
即β=π-2α,所以cosβ=cos(π-2α)=-cos2α=2sin2α-1=2×(
)2-1=
.
| 4 |
| 5 |
| 3 |
| 5 |
所以:cos(α+β)=cosα×cosβ-sinα×sinβ=
| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
由(1)知sinβ=
| 3 |
| 4 |
| 3 |
| 4 |
| 7 |
| 25 |
| 7 |
| 25 |
解法2:由 α为锐角,sinα=
| 4 |
| 5 |
| 3 |
| 5 |
此时cos(α+β)=-cosα=cos(π-α)而α,β为锐角,所以α+β=π-α
即β=π-2α,所以cosβ=cos(π-2α)=-cos2α=2sin2α-1=2×(
| 4 |
| 5 |
| 7 |
| 25 |
点评:本题是中档题,考查三角函数的化简求值,解答变换的技巧与应用,考查计算能力.

练习册系列答案
相关题目
已知
α、b 均为锐角,若p∶sinα<sin(α+b ), ,则p是q的
,则p是q的
[
]|
A .充分而不必要条件 |
B .必要而不充分条件 |
|
C .充要条件 |
D .即不充分也不必要条件 |
 ,则p是q的
,则p是q的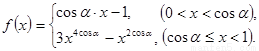 (其中
(其中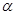 为锐角三角形的内角)且满足
为锐角三角形的内角)且满足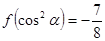 .
.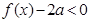 恒成立,求
恒成立,求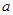 的取值范围.
的取值范围. ,α和β为锐角;
,α和β为锐角; ;求β;
;求β; )cot
)cot ,满足条件的α和β是否存在?若存在,请求出α和β的值;若不存在,请说明理由.
,满足条件的α和β是否存在?若存在,请求出α和β的值;若不存在,请说明理由.