题目内容
已知函数
的最大值为7，最小值为-1，求此函数式．
解：
显然y=m可以成立，当y≠m时，方程
必然有实数根，
∴△=48-4（y-m）（y-n）≥0，
即y2-（m+n）y+mn-12≤0，而-1≤y≤7
∴-1和7是方程y2-（m+n）y+mn-12=0的两个实数根
则
∴
分析：先去分母把其整理成关于X的一元二次方程的形式，再根据方程必然有实数根得到△=48-4（y-m）（y-n）≥0；最后根据函数的最大值为7，最小值为-1得到-1和7是方程y2-（m+n）y+mn-12=0的两个实数根；再结合根与系数的关系即可得到答案．
点评：本题考查一元二次方程的根的分布与系数的关系，考查分类讨论思想，转化思想，是中档题．
显然y=m可以成立，当y≠m时，方程
必然有实数根，
∴△=48-4（y-m）（y-n）≥0，
即y2-（m+n）y+mn-12≤0，而-1≤y≤7
∴-1和7是方程y2-（m+n）y+mn-12=0的两个实数根
则
∴
分析：先去分母把其整理成关于X的一元二次方程的形式，再根据方程必然有实数根得到△=48-4（y-m）（y-n）≥0；最后根据函数
的最大值为7，最小值为-1得到-1和7是方程y2-（m+n）y+mn-12=0的两个实数根；再结合根与系数的关系即可得到答案．点评：本题考查一元二次方程的根的分布与系数的关系，考查分类讨论思想，转化思想，是中档题．
练习册系列答案
相关题目
满足
，记目标函数
的最大值为7，则
；
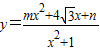的最大值为7，最小值为-1，求此函数式．
的最大值为7，最小值为-1，求此函数式．
的最大值为7，最小值为3，周期为8，在区间
上单调递减，且函数
图象过点P（5，5）。
的最小值；