题目内容
若方程2x2-4ax+3=0(a∈R)的两虚根分别是α、β,则|α|+|β|= .
分析:先假设两虚根,利用韦达定理求得它们的积,再计算相应的模即可
解答:解:假设两虚根为α=x+yi,β=x-yi(x,y∈R),则有αβ=x2+y2=
∵|α|+|β|= 2|α|=2
=
,∴|α|+|β|=
故答案为
| 3 |
| 2 |
∵|α|+|β|= 2|α|=2
|
| 6 |
| 6 |
故答案为
| 6 |
点评:本题的考点是复数相等的充要条件,主要考查实系数一元二次方程,虚根成对,考查复数的模,考查学生分析解决问题的能力.

练习册系列答案
相关题目
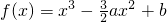 ,a,b为实数,x∈R,a∈R.
,a,b为实数,x∈R,a∈R. ,a,b为实数,x∈R,a∈R.
,a,b为实数,x∈R,a∈R.