Question

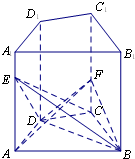如图，在直四棱柱ABCD-A₁B₁C₁D₁ 中，点E，F分别在AA₁，CC₁上，且AE=

3

4

AA₁，CF=

1

3

CC₁，点A，C到BD的距离之比为3：2，则三棱锥E-BCD和F-ABD的体积比

VE-ECD

VF-ABD

=

3

2

．

Answer 1

分析：根据A、C到BD的距离之比算出S_△BCD=

2

3

S_△ABD．由直四棱柱ABCD-A₁B₁C₁D₁ 中，AE=

3

4

AA₁且CF=

1

3

CC₁，算出AE=

9

4

CF，再由锥体的体积公式加以计算即可得到

VE-ECD

VF-ABD

的值．

解答：解：∵点A、C到BD的距离之比为3：2，
∴△BCD和△ABD的面积之比为3：2，可得S_△BCD=

2

3

S_△ABD
∵AE=

3

4

AA₁，CF=

1

3

CC₁，∴

AE

CF

=

3 4

1 3

=

9

4

∵三棱锥E-BCD的体积V₁=

1

3

S_△BCD•AE，三棱锥F-ABD的体积V₂=

1

3

S_△ABD•CF
∴

VE-ECD

VF-ABD

=

V1

V2

=

1 3 S△BCD•AE

1 3 S△ACD•CF

=

S△BCD

S△ACD

•

AE

CF

=

2

3

•

9

4

=

3

2

故答案为：

3

2

点评：本题给出直棱棱柱上满足条件的点，求两个三棱锥的体积之比．着重考查了直棱柱的性质、三角形的面积比和锥体的体积公式等知识，属于中档题．