题目内容
已知P是双曲线 的右支上一点,A1,A2分别为双曲线的左、右顶点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为e,有下列命题:①双曲线的一条准线被它的两条渐近线所截得的线段长度为
的右支上一点,A1,A2分别为双曲线的左、右顶点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为e,有下列命题:①双曲线的一条准线被它的两条渐近线所截得的线段长度为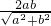 ;
;
②若|PF1|=e|PF2|,则e的最大值为 ;③△PF1F2的内切圆的圆心横坐标为a;④若直线PF1的斜率为k,则e2-k2>1,其中正确命题的序号是________.
;③△PF1F2的内切圆的圆心横坐标为a;④若直线PF1的斜率为k,则e2-k2>1,其中正确命题的序号是________.
①③④
分析:求出准线被它的两条渐近线所截得的线段的端点的纵坐标,即可得到此准线被它的两条渐近线所截得的线段
长度为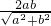 ,故①正确.
,故①正确.
由双曲线的定义可得 2a-|PF2|=e|PF2|,根据|PF2|=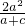 ≥c-a,求得
≥c-a,求得  ≤
≤ ,故②不正确.
,故②不正确.
由双曲线的定义及圆的切线性质可得|KF1|=a+c,故△PF1F2的内切圆的圆心横坐标为a,故③正确.
由题意可得k< ,故e2-k2>1,故④正确.
,故e2-k2>1,故④正确.
解答:对于①,一准线方程为x= ,它的两条渐近线方程为 y=±
,它的两条渐近线方程为 y=± x,
x,
故准线被它的两条渐近线所截得的线段的端点的纵坐标分别为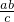 =±
=±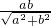 ,
,
故此线段的长度为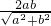 ,故①正确.
,故①正确.
对于②,若|PF1|=e|PF2|,则由双曲线的定义可得 2a-|PF2|=e|PF2|,
∴|PF2|= =
=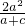 ≥c-a,∴3a2≥c2,∴
≥c-a,∴3a2≥c2,∴ ≤
≤ ,即离心率的最大值为
,即离心率的最大值为 ,故②不正确.
,故②不正确.
对于③,设△PF1F2的内切圆与PF1和PF2的切点分别为M,N,与x轴的切点为K,
由双曲线的定义及圆的切线性质可得|MF1|-|NF2|=2a=|KF1|-|KF2|,
又|KF1|+|KF2|=2c,∴|KF1|=a+c,故K为双曲线的右顶点,又△PF1F2的内切圆的圆心
在切点K 的正上方,故△PF1F2的内切圆的圆心横坐标为a,故③正确.
对于④若直线PF1的斜率为k,则由题意可得k< ,∴k2<
,∴k2<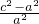 ,∴e2-k2>1,故④正确.
,∴e2-k2>1,故④正确.
故答案为:①③④.
点评:本题考查双曲线的标准方程,以及双曲线的简单性质的应用,熟练掌握双曲线的性质,是解题的关键.
分析:求出准线被它的两条渐近线所截得的线段的端点的纵坐标,即可得到此准线被它的两条渐近线所截得的线段
长度为
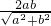 ,故①正确.
,故①正确.由双曲线的定义可得 2a-|PF2|=e|PF2|,根据|PF2|=
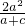 ≥c-a,求得
≥c-a,求得  ≤
≤ ,故②不正确.
,故②不正确.由双曲线的定义及圆的切线性质可得|KF1|=a+c,故△PF1F2的内切圆的圆心横坐标为a,故③正确.
由题意可得k<
 ,故e2-k2>1,故④正确.
,故e2-k2>1,故④正确.解答:对于①,一准线方程为x=
 ,它的两条渐近线方程为 y=±
,它的两条渐近线方程为 y=± x,
x,故准线被它的两条渐近线所截得的线段的端点的纵坐标分别为
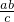 =±
=±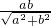 ,
,故此线段的长度为
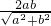 ,故①正确.
,故①正确.对于②,若|PF1|=e|PF2|,则由双曲线的定义可得 2a-|PF2|=e|PF2|,
∴|PF2|=
 =
=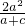 ≥c-a,∴3a2≥c2,∴
≥c-a,∴3a2≥c2,∴ ≤
≤ ,即离心率的最大值为
,即离心率的最大值为 ,故②不正确.
,故②不正确.对于③,设△PF1F2的内切圆与PF1和PF2的切点分别为M,N,与x轴的切点为K,
由双曲线的定义及圆的切线性质可得|MF1|-|NF2|=2a=|KF1|-|KF2|,
又|KF1|+|KF2|=2c,∴|KF1|=a+c,故K为双曲线的右顶点,又△PF1F2的内切圆的圆心
在切点K 的正上方,故△PF1F2的内切圆的圆心横坐标为a,故③正确.
对于④若直线PF1的斜率为k,则由题意可得k<
 ,∴k2<
,∴k2<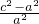 ,∴e2-k2>1,故④正确.
,∴e2-k2>1,故④正确.故答案为:①③④.
点评:本题考查双曲线的标准方程,以及双曲线的简单性质的应用,熟练掌握双曲线的性质,是解题的关键.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
 的右支上一点,A1, A2分别为双曲线的左、右顶点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为
的右支上一点,A1, A2分别为双曲线的左、右顶点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为 ,有下列命题:
,有下列命题: ;
; ;
; 的内切圆的圆心横坐标为
的内切圆的圆心横坐标为 ;
;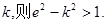
 的右支上一点,A1,A2分别为双曲线的左、右顶点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为e,有下列命题:
的右支上一点,A1,A2分别为双曲线的左、右顶点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为e,有下列命题:
 ,则e的最大值为
,则e的最大值为
 的内切圆的圆心横坐标为a;
的内切圆的圆心横坐标为a;
 的右支上一点,A1,A2分别为双曲线的左、右顶点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为e,有下列命题:①双曲线的一条准线被它的两条渐近线所截得的线段长度为
的右支上一点,A1,A2分别为双曲线的左、右顶点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为e,有下列命题:①双曲线的一条准线被它的两条渐近线所截得的线段长度为 ;
; ;③△PF1F2的内切圆的圆心横坐标为a;④若直线PF1的斜率为k,则e2-k2>1,其中正确命题的序号是 .
;③△PF1F2的内切圆的圆心横坐标为a;④若直线PF1的斜率为k,则e2-k2>1,其中正确命题的序号是 .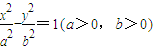 的右支上一点,A1,A2分别为双曲线的左、右顶点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为e,有下列命题:①双曲线的一条准线被它的两条渐近线所截得的线段长度为
的右支上一点,A1,A2分别为双曲线的左、右顶点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为e,有下列命题:①双曲线的一条准线被它的两条渐近线所截得的线段长度为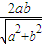 ;
;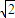 ;③△PF1F2的内切圆的圆心横坐标为a;④若直线PF1的斜率为k,则e2-k2>1,其中正确命题的序号是 .
;③△PF1F2的内切圆的圆心横坐标为a;④若直线PF1的斜率为k,则e2-k2>1,其中正确命题的序号是 . 的右支上一点,A1,A2分别为双曲线的左、右顶点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为e,有下列命题:
的右支上一点,A1,A2分别为双曲线的左、右顶点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为e,有下列命题: ;
; ;
;