题目内容
如图,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,∠BAD= 60°。
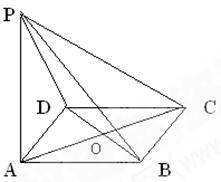
(1)求证:平面PBD⊥平面PAC;
(2)求点A到平面PBD的距离;
(3)求二面角B—PC—A的大小。(14分)

(1)求证:平面PBD⊥平面PAC;
(2)求点A到平面PBD的距离;
(3)求二面角B—PC—A的大小。(14分)
(1)略(2)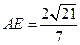 (3)
(3)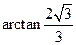
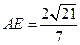 (3)
(3)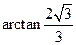
(1) 证: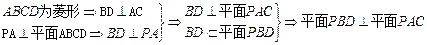 …4分
…4分
(2) 解:连结PO,过A作AE⊥PO,平面PAC 平面PBD=PO
平面PBD=PO
∴AE⊥平面PBD,AE就是所求的距离,计算得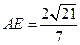 ……8分
……8分
(3) 解:过O作OF⊥PC,连BF,∵OB⊥平面PAC,由三垂线定理,PC⊥BF,
∴∠OFB为二面角B-PC-A的平面角,经计算得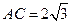 ,
,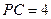 ,
,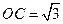 ,
,
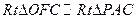 ∴
∴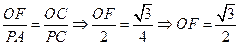
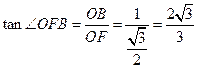 ∴
∴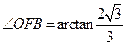 ,所求二面角大小为
,所求二面角大小为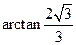 …14分
…14分
解法二:如图,以A原点,AB为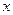 轴正方向,建立空间直角坐标系,则
轴正方向,建立空间直角坐标系,则 ,
,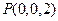 ,
,
过D作DE⊥AB于E,则DE=ADsin60°=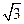 , AE=ADcos60°=1,∴
, AE=ADcos60°=1,∴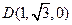 ,
,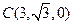 ,
,
(1)设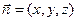 是平面PBD的法向量,则
是平面PBD的法向量,则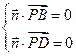 ,
,
又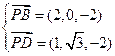 ,∴
,∴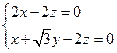 令
令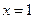 则
则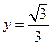 ,
,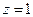 ,∴
,∴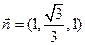
设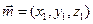 是平面PAC的法向量,则
是平面PAC的法向量,则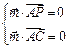 ,又
,又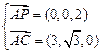 ,∴
,∴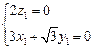
∴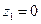 令
令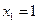 则
则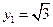 ,∴
,∴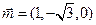 , ∵
, ∵ ∴
∴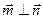 ,∴平面PBD⊥平面PAC(2)所求距离为
,∴平面PBD⊥平面PAC(2)所求距离为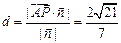
(3)设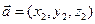 是平面PBC的法向量,则
是平面PBC的法向量,则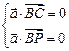 ,
,
又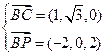 ,∴
,∴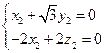 令
令 则
则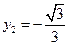 ,
,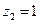 ,∴
,∴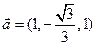
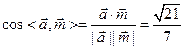 ,即二面角B-PC-A的大小为
,即二面角B-PC-A的大小为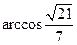 .
.
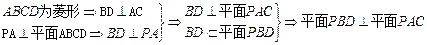 …4分
…4分(2) 解:连结PO,过A作AE⊥PO,平面PAC
 平面PBD=PO
平面PBD=PO∴AE⊥平面PBD,AE就是所求的距离,计算得
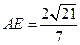 ……8分
……8分(3) 解:过O作OF⊥PC,连BF,∵OB⊥平面PAC,由三垂线定理,PC⊥BF,
∴∠OFB为二面角B-PC-A的平面角,经计算得
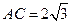 ,
,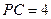 ,
,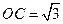 ,
,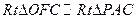 ∴
∴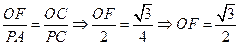
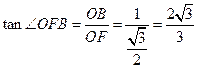 ∴
∴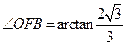 ,所求二面角大小为
,所求二面角大小为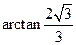 …14分
…14分解法二:如图,以A原点,AB为
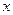 轴正方向,建立空间直角坐标系,则
轴正方向,建立空间直角坐标系,则 ,
,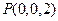 ,
,过D作DE⊥AB于E,则DE=ADsin60°=
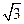 , AE=ADcos60°=1,∴
, AE=ADcos60°=1,∴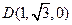 ,
,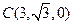 ,
,(1)设
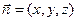 是平面PBD的法向量,则
是平面PBD的法向量,则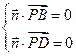 ,
,又
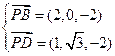 ,∴
,∴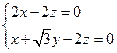 令
令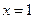 则
则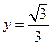 ,
,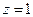 ,∴
,∴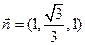
设
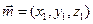 是平面PAC的法向量,则
是平面PAC的法向量,则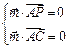 ,又
,又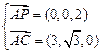 ,∴
,∴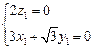
|
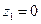 令
令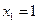 则
则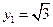 ,∴
,∴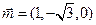 , ∵
, ∵ ∴
∴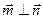 ,∴平面PBD⊥平面PAC(2)所求距离为
,∴平面PBD⊥平面PAC(2)所求距离为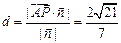
(3)设
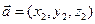 是平面PBC的法向量,则
是平面PBC的法向量,则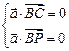 ,
,又
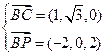 ,∴
,∴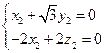 令
令 则
则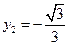 ,
,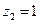 ,∴
,∴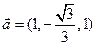
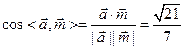 ,即二面角B-PC-A的大小为
,即二面角B-PC-A的大小为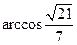 .
.
练习册系列答案
相关题目

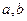 是两条不同的直线,
是两条不同的直线,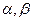 是两个不重合的平面,则下列命题中正确的是 ( )
是两个不重合的平面,则下列命题中正确的是 ( )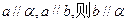
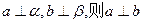
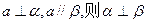
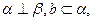 则
则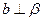
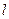 及两个平面
及两个平面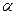 、
、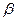 ,下列命题正确的是 ( )
,下列命题正确的是 ( )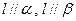 ,则
,则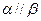
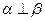
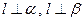 , 则
, 则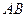 为圆柱下底面内任一不过圆心的弦,过
为圆柱下底面内任一不过圆心的弦,过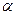 外一点,作与
外一点,作与