题目内容
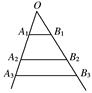
如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠BAD=60°,已知PB=PD=2,PA= .
.

(1)证明:PC⊥BD;
(2)若E为PA的中点,求三棱锥P-BCE的体积.
 .
.
(1)证明:PC⊥BD;
(2)若E为PA的中点,求三棱锥P-BCE的体积.
(1)见解析(2)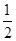
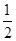
(1)证明:连接AC,交BD于点O,连接PO.
因为底面ABCD是菱形,所以AC⊥BD,BO=DO.
由PB=PD知,PO⊥BD.
又因为PO∩AC=O,所以BD⊥平面APC.
又PC?平面APC,因此BD⊥PC.
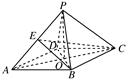
(2)因为E是PA的中点,
所以V三棱锥P-BCE=V三棱锥C-PEB=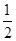 V三棱锥C-PAB=
V三棱锥C-PAB=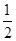 V三棱锥B-APC.
V三棱锥B-APC.
由PB=PD=AB=AD=2知,△ABD≌△PBD.
因为∠BAD=60°,
所以PO=AO=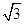 ,AC=2
,AC=2 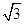 ,BO=1.
,BO=1.
又PA= ,所以PO2+AO2=PA2,所以PO⊥AC,
,所以PO2+AO2=PA2,所以PO⊥AC,
故S△APC=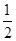 PO·AC=3.
PO·AC=3.
由(1)知,BO⊥平面APC,
因此V三棱锥P-BCE=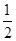 V三棱锥B-APC=
V三棱锥B-APC=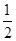 ·
·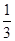 ·BO·S△APC=
·BO·S△APC=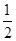 .
.
因为底面ABCD是菱形,所以AC⊥BD,BO=DO.
由PB=PD知,PO⊥BD.
又因为PO∩AC=O,所以BD⊥平面APC.
又PC?平面APC,因此BD⊥PC.

(2)因为E是PA的中点,
所以V三棱锥P-BCE=V三棱锥C-PEB=
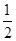 V三棱锥C-PAB=
V三棱锥C-PAB=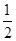 V三棱锥B-APC.
V三棱锥B-APC.由PB=PD=AB=AD=2知,△ABD≌△PBD.
因为∠BAD=60°,
所以PO=AO=
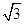 ,AC=2
,AC=2 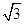 ,BO=1.
,BO=1.又PA=
 ,所以PO2+AO2=PA2,所以PO⊥AC,
,所以PO2+AO2=PA2,所以PO⊥AC,故S△APC=
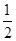 PO·AC=3.
PO·AC=3.由(1)知,BO⊥平面APC,
因此V三棱锥P-BCE=
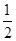 V三棱锥B-APC=
V三棱锥B-APC=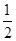 ·
·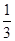 ·BO·S△APC=
·BO·S△APC=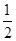 .
.
练习册系列答案
相关题目
 所在的平面和平面
所在的平面和平面 互相垂直,等腰梯形
互相垂直,等腰梯形 ∥
∥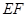 ,
, =2,
=2, ,
, ,
, ,
, 分别为
分别为 的中点,
的中点, 为底面
为底面 的重心.
的重心.
 平面
平面 ;
; ∥平面
∥平面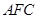 ;
; 的体积
的体积 .
.  (AC+BD)(填“>”“<”或“=”).
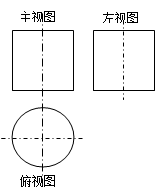
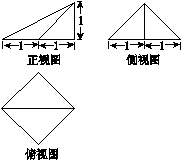
(AC+BD)(填“>”“<”或“=”). BB'=CC'=AB,则多面体ABC-A'B'C'的正视图是( )
BB'=CC'=AB,则多面体ABC-A'B'C'的正视图是( ) 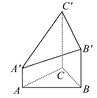

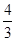 πr3,观察发现V′=S.则由四维空间中“超球”的三维测度V=8πr3,猜想其四维测度W=________.
πr3,观察发现V′=S.则由四维空间中“超球”的三维测度V=8πr3,猜想其四维测度W=________.