题目内容
求与两坐标轴围成的三角形周长为9,且斜率为-| 4 | 3 |
分析:设直线l的方程斜截式,求出它与两坐标轴的交点,利用与两坐标轴围成的三角形周长为9,求出待定系数,从而得到直线l的方程.
解答:解:设直线l的方程 y=-
x+b,则它与两坐标轴的交点(
b,0)、(0,b),
∵与两坐标轴围成的三角形周长为9,∴|
b|+|b|+
=9,
3|b|=9,∴b=±3.∴直线l的方程:y=-
x+3,或y=-
x-3.
即4x+3y-9=0,或 4x+3y+9=0.
| 4 |
| 3 |
| 3 |
| 4 |
∵与两坐标轴围成的三角形周长为9,∴|
| 3 |
| 4 |
(
|
3|b|=9,∴b=±3.∴直线l的方程:y=-
| 4 |
| 3 |
| 4 |
| 3 |
即4x+3y-9=0,或 4x+3y+9=0.
点评:本题考查直线方程的应用,利用直线方程求交点的坐标、线段的长度.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目

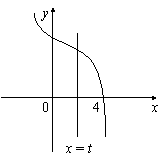 (2)若直线x = t
(0<t<4)将函数y = h (x)的图象与两坐标轴围成的图形的面积二等分,求t的值.
(2)若直线x = t
(0<t<4)将函数y = h (x)的图象与两坐标轴围成的图形的面积二等分,求t的值.