题目内容
(本小题满分12分)已知圆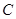 以
以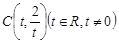 为圆心且经过原点O.
为圆心且经过原点O.
(1) 若直线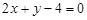 与圆
与圆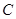 交于点
交于点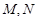 ,若
,若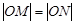 ,求圆
,求圆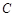 的方程;
的方程;
(2) 在(1)的条件下,已知点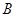 的坐标为
的坐标为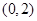 ,设
,设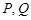 分别是直线
分别是直线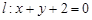 和圆
和圆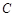 上的动点,求
上的动点,求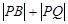 的最小值及此时点
的最小值及此时点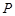 的坐标。
的坐标。
(1)圆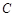 方程为
方程为 .(2)
.(2)  .
.
解析试题分析:(I)利用圆的标准方程写出圆的方程,根据线段的中垂线的性质判断出C,H,O三点共线,利用两点连线的斜率公式求出直线OC的斜率,列出关于t的方程,求出t的值.通过圆心到直线的距离与圆半径的大小的比较,判断出直线与圆的关系是否相交.
(II)求出点B关于直线x+y+2=0的对称点,将已知问题转化为对称点到圆上的最小值问题,根据圆的几何条件,圆外的点到圆上的点的最小值等于该点到圆心的距离减去半径.
考点:本题主要是考查直线与圆的位置关系的运用。
解:由题知,圆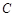 方程为
方程为 ,
,
化简得 …1分
…1分
(1) ,则原点
,则原点 在
在 的中垂线上,设
的中垂线上,设 的中点为
的中点为 ,则
,则 .
. 三点共线,则直线
三点共线,则直线 的斜率
的斜率 或
或 ,则圆心
,则圆心 或
或 , …4分
, …4分
所以圆方程为 或
或 , …5分
, …5分
由于当圆方程为 时,直线
时,直线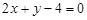 到圆心的距离
到圆心的距离 ,不满足直线和圆相交,故舍去.
,不满足直线和圆相交,故舍去. 圆
圆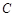 方程为
方程为 . …6分
. …6分
(2)点 关于直线
关于直线 的对称点为
的对称点为 , …7分
, …7分
则
 ,又
,又 到圆上点
到圆上点 的最短距离为
的最短距离为 ,
,
所以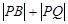 的最小值为
的最小值为 , …10分
, …10分
直线 的方程为
的方程为 ,则直线
,则直线 与直线
与直线 的
的
交点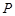 的坐标为
的坐标为 . …12分
. …12分
点评:解决该试题的关键是求圆的方程一般利用的方法是待定系数法;解决直线与圆的有关的问题常利用圆的一些几何意义:常需要解圆心距、弦长的一半、圆的半径构成的直角三角形;圆外的点到圆上的最值常求出点到圆心的距离加上或减去圆的半径
