题目内容
已知数列{an}的前n项和Sn=3n-1,数列{bn}满足b1=1,bn=3bn-1+an(n≥2),记数列{bn}的前n项和为Tn。
(Ⅰ)证明{an}为等比数列;
(Ⅱ)求Tn;
(Ⅲ)设Pn=Sn+Tn,若对于任意n∈N*,都有 成立,求实数λ的取值范围。
成立,求实数λ的取值范围。
(Ⅰ)证明{an}为等比数列;
(Ⅱ)求Tn;
(Ⅲ)设Pn=Sn+Tn,若对于任意n∈N*,都有
 成立,求实数λ的取值范围。
成立,求实数λ的取值范围。 解:(Ⅰ)证明:因为数列{an}的前,n项和S=3n-1,
所以an=Sn-Sn-1=(3n-1)-(3n-1-1) =2·3n-1(n≥2),
因为n=1时,a1=S1=2也适合上式,
所以an=2·3n-1(n∈N*),
因为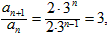 ,
,
所以数列{an}是首项为2,公比为3的等比数列;
(Ⅱ)当 n≥2时,bn=3bn-1+2-33n-1,
将其变形为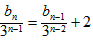 ,
,
即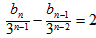
所以数列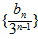 ,是首项为
,是首项为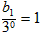 公差为2的等差数列,
公差为2的等差数列,
所以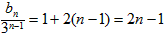
所以bn= (2n-1)·3n-1(n∈N*),
因为Tn=1×30+3×31+5×32+…+(2n-1). 3n-1,
所以3Tn=1×31+3×32+5×33+…+(2n-1)·3n,
两式相减得2Tn=-1-2(31+32+…+3n-1)+ (2n-1)·3n,
整理得Tn=(n-1)·3n+1(n∈N*);
(Ⅲ)由Pn=Sn+Tn=n·3n,得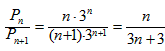
于是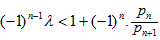
化为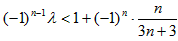 (*)
(*)
①当n是正奇数时,(*)式可化为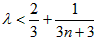 ,
,
显然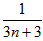 ,大于0,且随着正奇数n的增大而减小,
,大于0,且随着正奇数n的增大而减小,
由于(*)式对任意正奇数n恒成立,
所以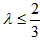 ,
,
②当n是正偶数时,(*)式可化为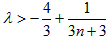 ,
,
显然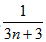 随着正偶数n的增大而减小,
随着正偶数n的增大而减小,
由于(*)式对任意正偶数n恒成立,
所以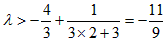 ,
,
综上,实数λ的取值范围是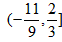 。
。

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |