题目内容
“
”是“
”成立的 条件.（从“充要”、“充分不必要”、“必要不充分”中选择一个正确的填写）
充分不必要
解析试题分析：由，又因为对数函数
在定义域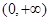
单调递增，所以；当，由于不知道
是否为正数，所以
不一定有意义.故不能推出
，所以”是“”成立的充分不必要条件.
考点：对数函数的单调性、充分必要条件
练习册系列答案
相关题目
题目内容
“”是“”成立的 条件.（从“充要”、“充分不必要”、“必要不充分”中选择一个正确的填写）
充分不必要
解析试题分析：由，又因为对数函数在定义域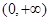单调递增，所以；当，由于不知道是否为正数，所以不一定有意义.故不能推出
，所以”是“”成立的充分不必要条件.
考点：对数函数的单调性、充分必要条件
（
），则f（sinθ）<
；③若f（x）的图像在点A(1,f(1))处的切线方程是y=
x+2，则f(1)+f '（1）=3；
-x),则f(lg2)+f(lg
在区间（0,1）上有零点。
∈R，
－2ax＋a≤0”为假命题，则
的最小值是__________．
”以及它的逆命题，否命题，逆否命题中，真命题的个数是______________________．
:
，
:
，若
的取值范围．
”的否定是________．
中，若
，则
；
，则
在
上的投影为
；
，
，则“
”为假命题；
的图象，只需将
的图象向左平移
个单位．
:
,命题
:
,若
的取值范围是 . 
=3，则
≥3”，的否命题是________________．