题目内容
7．
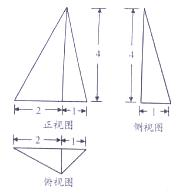若某几何体的三视图如图所示，则该几何体的体积为（ ）| A． | 1 | B． | $\frac{4}{3}$ | C． | 2 | D． | 6 |
分析 由已知中的三视图，我们可以判断出几何体的形状，进而求出几何体的底面面积和高后，代入棱锥体积公式，可得答案．
解答 解：由已知中的三视图可得几何体是一个三棱锥，
且棱锥的底面是一个以（2+1）=3为底，以1为高的三角形，棱锥的高为4．
故棱锥的体积V=$\frac{1}{3}$•$\frac{1}{2}$•（2+1）•1•4=2
故选：C．
点评 本题考查的知识点是由三视图求体积，其中根据已知判断出几何体的形状是解答本题的关键．
练习册系列答案
相关题目
17．在某项测量中，测量结果X服从正态分布N（2，σ2），若X在（0，4）内取值的概率为0.6，则X在（0，2）内取值的概率为（ ）
| A． | 0.2 | B． | 0.3 | C． | 0.4 | D． | 0.6 |
15．若不等式|ax+1|≤3的解集为{x|-2≤x≤1}，则实数a=（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
2．已知平面α，β，且α∥β，若$\overrightarrow{a}$=（1，λ，2），$\overrightarrow{b}$=（-3，6，-6）分别是两个平面α，β的法向量，则实数λ的值为-2．
12．函数f（x）=x3-3x的单调递减区间为（ ）
| A． | （0，+∞） | B． | （-∞，0） | C． | （-1，1） | D． | （1，+∞） |
19．在极坐标系中，直线ρcosθ=1与圆ρ=2cosθ的位置关系是（ ）
| A． | 相离 | B． | 相切 | C． | 相交但不过圆心 | D． | 相交且过圆心 |