题目内容
(1)选修4-2:矩阵与变换已知矩阵
 ,若矩阵A属于特征值6的一个特征向量为
,若矩阵A属于特征值6的一个特征向量为 ,属于特征值1的一个特征向量为
,属于特征值1的一个特征向量为 ,求矩阵A.
,求矩阵A.(2)选修4-4:坐标与参数方程
以直角坐标系的原点为极点,x轴正半轴为极轴,并在两种坐标系中取相同的长度单位.已知直线l的极坐标方程为psin(
 )=6,圆C的参数方程为
)=6,圆C的参数方程为 ,(θ为参数),求直线l被圆C截得的弦长.
,(θ为参数),求直线l被圆C截得的弦长.(3)选修4-5:不等式选讲
已知实数a,b,c,d满足a+b+c+d=3,a2+2b2+3c2+6d2=5试求a的最值.
【答案】分析:(1)依题意得 ,得到关于c,d的方程组,即可求得矩阵A;
,得到关于c,d的方程组,即可求得矩阵A;
(2)先将曲线的参数方程化成普通方程,再利用圆的几何性质,结合点到直线的距离公式即可求得直线l被圆截得的弦长.
(3)首先分析题目已知a2+2b2+3c2+6d2=5,可以考虑到柯西不等式的应用,建立关于a的不等关系后,再根据不等式的解法即可.
解答:解:(1)依题意得 ,即
,即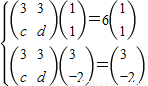
所以 解得
解得 ∴
∴
(2)由ρsin(θ-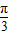 )=ρ(
)=ρ( sinθ-
sinθ- cosθ)=6,∴
cosθ)=6,∴
将圆的参数方程化为普通方程为x2+y2=10圆心为C(0,0),半径为10.
∴点C到直线的距离为d= ,
,
直线l被圆截得的弦长为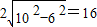
(3)由柯西不等式得,有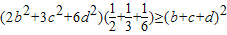
即2b2+3c2+6d2≥(b+c+d)2,由条件可得,5-a2≥(3-a)2
解得,1≤a≤2,代入 时,amax=2;
时,amax=2; 时,amin=1
时,amin=1
点评:本题主要考查了二阶矩阵、考查圆的参数方程、参数方程的概念、直线与圆相交的性质、不等式的证明问题,其中涉及到柯西不等式和基本不等式的应用问题,有一定的技巧性,需要同学们对两种不等式非常熟练,属于中档题目.
 ,得到关于c,d的方程组,即可求得矩阵A;
,得到关于c,d的方程组,即可求得矩阵A;(2)先将曲线的参数方程化成普通方程,再利用圆的几何性质,结合点到直线的距离公式即可求得直线l被圆截得的弦长.
(3)首先分析题目已知a2+2b2+3c2+6d2=5,可以考虑到柯西不等式的应用,建立关于a的不等关系后,再根据不等式的解法即可.
解答:解:(1)依题意得
 ,即
,即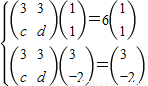
所以
 解得
解得 ∴
∴
(2)由ρsin(θ-
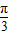 )=ρ(
)=ρ( sinθ-
sinθ- cosθ)=6,∴
cosθ)=6,∴
将圆的参数方程化为普通方程为x2+y2=10圆心为C(0,0),半径为10.
∴点C到直线的距离为d=
 ,
,直线l被圆截得的弦长为
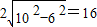
(3)由柯西不等式得,有
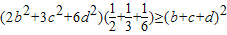
即2b2+3c2+6d2≥(b+c+d)2,由条件可得,5-a2≥(3-a)2
解得,1≤a≤2,代入
 时,amax=2;
时,amax=2; 时,amin=1
时,amin=1点评:本题主要考查了二阶矩阵、考查圆的参数方程、参数方程的概念、直线与圆相交的性质、不等式的证明问题,其中涉及到柯西不等式和基本不等式的应用问题,有一定的技巧性,需要同学们对两种不等式非常熟练,属于中档题目.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,PB交AC于点E,交⊙O于点D,若PE=PA,
如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,PB交AC于点E,交⊙O于点D,若PE=PA, ,PD=1,BD=8,求线段BC的长.
,PD=1,BD=8,求线段BC的长. ,矩阵阵
,矩阵阵 ,
, ,求在矩阵
,求在矩阵 作用下变换所得到的图形的面积.
作用下变换所得到的图形的面积. (
( 为参数,
为参数, 为常数且
为常数且 )被以原点为极点,
)被以原点为极点, 轴的正半轴为极轴,方程为
轴的正半轴为极轴,方程为 的曲线所截,求截得的弦长.
的曲线所截,求截得的弦长. ,求证:
,求证: .
.