题目内容
A
解:(1)依题意知,f(x)的定义域为(0,+∞).
当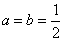 时,f(x)=lnx-
时,f(x)=lnx-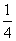 x2-
x2- x,f′(x)=
x,f′(x)=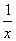 -
- x-
x- =
=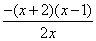 ,
,
令f′(x)=0,解得x=1或x=-2(舍去).…………2分
当0<x<1时,f′(x)>0,当x>1时,f′(x)<0,
所以f(x)的单调递增区间为(0,1),单调递减区间为(1,+∞).
(2)F(x)=lnx+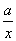 ,x∈(0,3],
,x∈(0,3],
则有k=F′(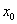 )=
)=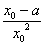 ≤
≤ 在(0,3]上恒成立.
在(0,3]上恒成立.
所以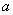
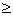
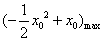 ,
,
当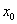 =1时,-
=1时,- x
x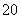 +
+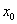 取得最大值
取得最大值 .
. 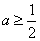 .
.
(3)当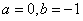 时,f(x)=lnx+x,
时,f(x)=lnx+x,
由f(x)=mx,得lnx+x=mx,
又x>0,∴m=1+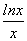 .
.
要使方程f(x)=mx在区间上有唯一实数解.
只需m=1+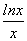 有唯一实数解,令g(x)=1+
有唯一实数解,令g(x)=1+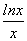 (x>0),∴g′(x)=
(x>0),∴g′(x)=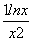 ,
,
由g′(x)>0,得0<x<e.g′(x)<0,得x>e,
∴g(x)在区间上是增函数,在区间上是减函数.
g(1)=1,g(e2)=1+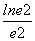 =1+
=1+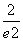 ,g(e)=1+
,g(e)=1+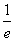 ,
,
∴m=1+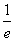 或1≤m<1+
或1≤m<1+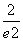 .
.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
下表是降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对应数据,根据表中提供的数据,求出y关于x的线性回归方程为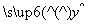 =0.7x+0.35,那么表中m值为( ).
=0.7x+0.35,那么表中m值为( ).
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | m | 4 | 4.5 |
A. 3 B.3.15 C.4 D.4.5
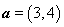 ,若
,若 ,则实数
,则实数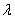 的值为
的值为 B.
B.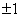 C.
C.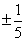 D. 1
D. 1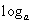 (2x2-1)的导数是( )
(2x2-1)的导数是( )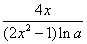 B.
B. 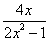 C.
C. 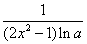 D.
D. 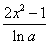
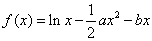
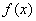 的单调区间;
的单调区间;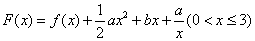 ,其图象上任意一点P(x0,y0)处切线的斜率k≤
,其图象上任意一点P(x0,y0)处切线的斜率k≤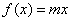 在区间内有唯一实数解,求实数
在区间内有唯一实数解,求实数 的取值范围.
的取值范围. ( )
( )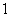 B.-
B.-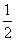 C.
C.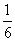 D.
D.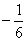
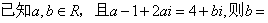
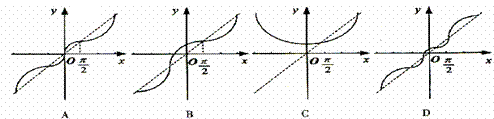 ( )
( )