题目内容
设a,b是两个实数,且a≠b,①a5+b5>a3b2+a2b3,②a2+b2≥2(a-b-1),③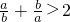 .上述三个式子恒成立的有
.上述三个式子恒成立的有
- A.0个
- B.1个
- C.2个
- D.3个
B
分析:对于①,欲证a5+b5>a2b3+a3b2,只要证a5+b5-a2b3+a3b2>0即可,移项后利用二次式的配方法即可;对于②,左右作差后配成完全平方后即得;对于③,因为a,b不一定是同号,不能直接利用基本不等式得到.
解答:①a5+b5-a3b2-a2b3=a3(a2-b2)+b3(b2-a2)
=(a2-b2)(a3-b3)=(a+b)(a-b)2(a2+ab+b2).
∵(a-b)2≥0,a2+ab+b2≥0,但a+b符号不确定,
∴a5+b5>a3b2+a2b3不正确;
故从条件来看,①不一定成立;
②a2+b2-2a+2b+2=(a-1)2+(b+1)2≥0,
∴a2+b2≥2(a-b-1);成立;
③因为a,b不一定是同号,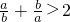 不正确.
不正确.
正确的为:②.
故选B.
点评:本题主要考查了不等式,涉及到基本不等式、作差比较法、二次函数的配方法等,属于基础题.本题主要考查不等式的证明,从已知条件出发,利用定义、公理、定理、某些已经证明过的不等式及不等式的性质经过一系列的推理、论证等而推导出所要证明的不等式,这个证明方法叫综合法.
分析:对于①,欲证a5+b5>a2b3+a3b2,只要证a5+b5-a2b3+a3b2>0即可,移项后利用二次式的配方法即可;对于②,左右作差后配成完全平方后即得;对于③,因为a,b不一定是同号,不能直接利用基本不等式得到.
解答:①a5+b5-a3b2-a2b3=a3(a2-b2)+b3(b2-a2)
=(a2-b2)(a3-b3)=(a+b)(a-b)2(a2+ab+b2).
∵(a-b)2≥0,a2+ab+b2≥0,但a+b符号不确定,
∴a5+b5>a3b2+a2b3不正确;
故从条件来看,①不一定成立;
②a2+b2-2a+2b+2=(a-1)2+(b+1)2≥0,
∴a2+b2≥2(a-b-1);成立;
③因为a,b不一定是同号,
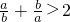 不正确.
不正确.正确的为:②.
故选B.
点评:本题主要考查了不等式,涉及到基本不等式、作差比较法、二次函数的配方法等,属于基础题.本题主要考查不等式的证明,从已知条件出发,利用定义、公理、定理、某些已经证明过的不等式及不等式的性质经过一系列的推理、论证等而推导出所要证明的不等式,这个证明方法叫综合法.

练习册系列答案
相关题目