Question

如图，四边形ABCD为正方形，PD⊥平面ABCD，PD=AD=2．
（1）求PC与平面PBD所成的角；
（2）在线段PB上是否存在一点E，使得PC⊥平面ADE？并说明理由．

Answer 1

解：连接AC，设AC∩BD=O，连接PO
∵PD⊥平面ABCD，CO?平面ABCD∴PD⊥CO
由ABCD为正方形，知CO⊥BD
∵PD∩BD=D∴CO⊥平面PBD
∴∠CPO是直线PC与平面PBD所成的角
在Rt△POC中，=
∴
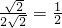
∴直线PC与平面PBD所成的角为
（2）建立如图所示的空间直角坐标系D_xyz，设线段PB上存在一点E，使得PC⊥平面ADE
则存在实数λ，使得（0≤λ≤1）
∵P（0，0，2），B（2，2，0）∴
∴==（2λ，2λ，2-2λ）
由题意显然有AD⊥平面PCD∴PC⊥AD 要使PC⊥平面ADE，只需
即∴0×2λ+2×2λ-2（2-2λ）=0
∴
故在线段上存在一点E（E为线段的中点）使得PC⊥平面ADE
分析：要求PC与平面PBD所成的角，直线找出已知平面PBD的垂线，设AC∩BD=O，由PD⊥平面ABCD，可得PD⊥CO，容易证明CO⊥BD
CO⊥平面PBD，∠CPO是直线PC与平面PBD所成的角在Rt△POC中，由可求
（2）由于存在性问题的特点，考虑利用空间向量法，先建立如图所示的空间直角坐标系D_xyz，设线段PB上存在一点E，使得PC⊥平面ADE、，则由向量的共线定理可得，存在实数λ，使得（0≤λ≤1），则．然后由AD⊥平面PCD，可得PC⊥AD，要使PC⊥平面ADE，只需，即，从而可求λ，进而判断是否存在
点评：本题主要考查了直线与平面所成的角的求解，这是立体几何中最基本的试题类型，而在立体几何图形中，存在性问题的求解一般采用向量法求解比较容易．