题目内容
如图已知点A（1，-1）和单位圆上半部分上的动点B，则|| OA |
| OB |
分析：由题意利用单位圆的性质，设B（cosα，sinα）（0≤α≤π），从而得到
+
=（1+cosα，-1+sinα）．再根据向量模的公式、三角恒等变换和正弦函数的图象与性质加以计算，可得当α=0时|
+
|2的最大值为5，由此可得|
+
|的最大值．
| OA |
| OB |
| OA |
| OB |
| OA |
| OB |
解答：解：∵动点B在单位圆的上半部分，
∴设B（cosα，sinα），得
=（cosα，sinα），其中0≤α≤π
∵
=（1，-1），∴
+
=（1+cosα，-1+sinα），
可得|
+
|2=（1+cosα）2+（-1+sinα）2
=（1+2cosα+cos2α）+（1-2sinα+sin2α）=3+2（cosα-sinα），
∵cosα-sinα=
sin（
-α），
-α∈[-
，
]，
∴当
-α=
即α=0时，cosα-sinα有最大值为1．
由此可得|
+
|2=3+2（cosα-sinα）的最大值为3+2=5．
∴|
+
|的最大值为
故选：A
∴设B（cosα，sinα），得
| OB |
∵
| OA |
| OA |
| OB |
可得|
| OA |
| OB |
=（1+2cosα+cos2α）+（1-2sinα+sin2α）=3+2（cosα-sinα），
∵cosα-sinα=
| 2 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
∴当
| π |
| 4 |
| π |
| 4 |
由此可得|
| OA |
| OB |
∴|
| OA |
| OB |
| 5 |
故选：A
点评：本题给出单位圆上的动点B与定点A，求|
+
|的最大值．着重考查了向量的坐标运算、向量模的公式和三角函数的最值求法等知识，属于中档题．
| OA |
| OB |
练习册系列答案
培优三好生系列答案
优化作业上海科技文献出版社系列答案
相关题目
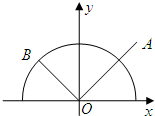如图，已知点A（1，1）和单位圆上半部分上的动点B．
如图，已知点A（-1，0）与点B（1，0），C是圆x2+y2=1上的动点，连接BC并延长至D，使得|CD|=|BC|，求AC与OD的交点P的轨迹方程．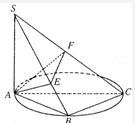
如图已知点B在以AC为直径的圆上，SA⊥面ABC，AE⊥SB于E，AF⊥SC于F．
如图已知椭圆