题目内容
已知函数f(x)的图象与函数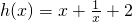 的图象关于点A(0,1)对称,则当
的图象关于点A(0,1)对称,则当 时,f(x)的值域为
时,f(x)的值域为
- A.

- B.
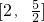
- C.

- D.[2,+∞)
C
分析:先设函数f(x)的图象上任意一点P(x,y),根据它关于点A(0,1)对称的点的坐标为Q(-x,2-y),利用题意Q点在函数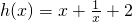 的图象上,求出函数f(x)的解析式,最后利用其解析式求出f(x)的值域.
的图象上,求出函数f(x)的解析式,最后利用其解析式求出f(x)的值域.
解答:设函数f(x)的图象上任意一点P(x,y),
它关于点A(0,1)对称的点的坐标为Q(-x,2-y),
根据题意Q点在函数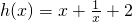 的图象上,
的图象上,
则2-y=-x+ +2,
+2,
∴y=x+ ,即f(x)=x+
,即f(x)=x+ ,
, .
.
当x=1时,f(x)取得最小值2,当x=3时,f(x)取得最大值 ,
,
∴当 时,f(x)的值域
时,f(x)的值域 .
.
故选C.
点评:本小题主要考查函数单调性的应用、函数对称性的应用、函数的值域等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.
分析:先设函数f(x)的图象上任意一点P(x,y),根据它关于点A(0,1)对称的点的坐标为Q(-x,2-y),利用题意Q点在函数
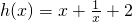 的图象上,求出函数f(x)的解析式,最后利用其解析式求出f(x)的值域.
的图象上,求出函数f(x)的解析式,最后利用其解析式求出f(x)的值域.解答:设函数f(x)的图象上任意一点P(x,y),
它关于点A(0,1)对称的点的坐标为Q(-x,2-y),
根据题意Q点在函数
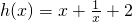 的图象上,
的图象上,则2-y=-x+
 +2,
+2,∴y=x+
 ,即f(x)=x+
,即f(x)=x+ ,
, .
.当x=1时,f(x)取得最小值2,当x=3时,f(x)取得最大值
 ,
,∴当
 时,f(x)的值域
时,f(x)的值域 .
.故选C.
点评:本小题主要考查函数单调性的应用、函数对称性的应用、函数的值域等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
相关题目
已知函数f(x)的图象关于直线x=2对称,且当x≠2时其导函数f′(x)满足xf′(x)>2f′(x),若2<a<4,则下列表示大小关系的式子正确的是( )
| A、f(2a)<f(3)<f(log2a) | B、f(3)<f(log2a)<f(2a) | C、f(log2a)<f(3)<f(2a) | D、f(log2a)<f(2a)<f(3) |
 (2011•焦作一模)已知函数f(x)的图象过点(
(2011•焦作一模)已知函数f(x)的图象过点(