题目内容
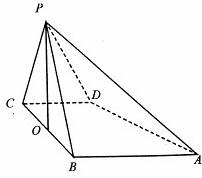 如图,四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=PB=PC=2CD=2,PO⊥AD,O为BC的中点.
如图,四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=PB=PC=2CD=2,PO⊥AD,O为BC的中点.(Ⅰ)求证:PO⊥底面ABCD;
(Ⅱ)求二面角P-AD-B的大小.
(Ⅲ)求直线PB与平面PAD所成的线面角的大小.
分析:法一:(Ⅰ)要证PO⊥底面ABCD,只需证明直线PO垂直底面ABCD内的两条相交直线BC、AD即可;
(Ⅱ)过点O作OE⊥AD于点E,连接PE,说明∴∠PEO为二面角P-AD-B的平面角,
解三角形求二面角P-AD-B的大小.
(Ⅲ)取PA、PB的中点M、N,连接BM、CN、DM、MN,
说明直线PB与平面PAD所成的线面角为∠BPM,然后求解即可得到
直线PB与平面PAD所成的线面角的大小.
法二:以BC中点O为原点,以BC所在直线为x轴,过点O与AB平行的直线为y轴,
建立如图所示的空间直角坐标系O-xyz,
(Ⅱ)求出平面PAD的法向量,平面ABCD的法向量为
=(0,0,
)
然后利用向量的数量积求直线PB与平面PAD所成的线面角的大小.
(Ⅲ)求出相关向量,通过cos?
,
?=
求得
直线PB与平面PAD所成的线面角的大小.
(Ⅱ)过点O作OE⊥AD于点E,连接PE,说明∴∠PEO为二面角P-AD-B的平面角,
解三角形求二面角P-AD-B的大小.
(Ⅲ)取PA、PB的中点M、N,连接BM、CN、DM、MN,
说明直线PB与平面PAD所成的线面角为∠BPM,然后求解即可得到
直线PB与平面PAD所成的线面角的大小.
法二:以BC中点O为原点,以BC所在直线为x轴,过点O与AB平行的直线为y轴,
建立如图所示的空间直角坐标系O-xyz,
(Ⅱ)求出平面PAD的法向量,平面ABCD的法向量为
| OP |
| 3 |
然后利用向量的数量积求直线PB与平面PAD所成的线面角的大小.
(Ⅲ)求出相关向量,通过cos?
| PB |
| n1 |
| ||||
|
|
直线PB与平面PAD所成的线面角的大小.
解答: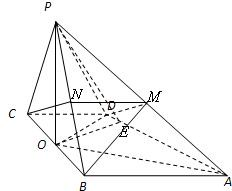 解法一:(Ⅰ)证明:∵PB=PC=BC,O为BC中点
解法一:(Ⅰ)证明:∵PB=PC=BC,O为BC中点
∴PO⊥BC
又∵PO⊥AD
而ABCD是直角梯形,从而BC与AD相交(没有说明扣1分)
∴PO⊥底面ABCD
(Ⅱ)∵PO⊥底面ABCD,过点O作OE⊥AD于点E,连接PE,由三垂线定理知PE⊥AD
∴∠PEO为二面角P-AD-B的平面角
∵AB=BC=PB=PC=2CD=2,O为BC中点
∴AO=AD=
,OD=
,PO=
由等面积法知S△AOD=
•AD•OE=
•OD•
?OE=
∴tan∠PEO=
=
∴∠PEO=arctan
,即二面角P-AD-B的大小为arctan
(或arcsin
或arccos
)
(Ⅲ)取PA、PB的中点M、N,连接BM、CN、DM、MN,
∵PC=BC,
∴CN⊥PB①
∵AB⊥BC,且PO⊥AB
∴AB⊥平面PBC
∵CN?平面PBC
∴CN⊥AB②
由①、②知CN⊥平面PAB
由MN∥AB∥CD,MN=AB=CD,得四边形MNCD为平行四边形
∴CN∥DM
∴DM⊥平面PAB
∵BM?平面PAD
∴DM⊥BM
∵PB=AB=2
∴BM⊥PA
∴BM⊥平面PAD,直线PB与平面PAD所成的线面角为∠BPM
在等腰直角三角形PAB中,易知∠BPM=45°
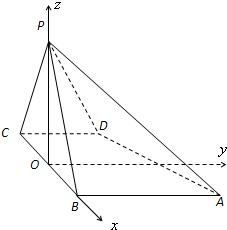 解法二:(Ⅰ)同解法一;
解法二:(Ⅰ)同解法一;
如图,以BC中点O为原点,以BC所在直线为x轴,
过点O与AB平行的直线为y轴,
建立如图所示的空间直角坐标系O-xyz.
(Ⅱ)∵BC=PB=PC=2且PO⊥底面ABCD
∴平面ABCD的法向量为
=(0,0,
)
∵A(1,2,0),D(-1,1,0),P(0,0,
)
∴
=(2,1,0),
=(1,2,-
)
设平面PAD的法向量为
=(x1,y1,z1),
由
得到
,
令x1=1,则y1=-2,z3=-
,即
=(1,-2,-
)
∴cos<
,
>=
=-
∴二面角P-AD-B的大小为arccos
(或arcsin
或arctan
)
(Ⅲ)∵B(1,0,0)
∴
=(1,0,-
)
由(Ⅱ)知平面PAD的法向量为
=(1,-2,-
)
则cos?
,
?=
=
=
,即?
,
?=450
所以直线PB与平面PAD所成的线面角为90°-45°=45°
 解法一:(Ⅰ)证明:∵PB=PC=BC,O为BC中点
解法一:(Ⅰ)证明:∵PB=PC=BC,O为BC中点∴PO⊥BC
又∵PO⊥AD
而ABCD是直角梯形,从而BC与AD相交(没有说明扣1分)
∴PO⊥底面ABCD
(Ⅱ)∵PO⊥底面ABCD,过点O作OE⊥AD于点E,连接PE,由三垂线定理知PE⊥AD
∴∠PEO为二面角P-AD-B的平面角
∵AB=BC=PB=PC=2CD=2,O为BC中点
∴AO=AD=
| 5 |
| 2 |
| 3 |
由等面积法知S△AOD=
| 1 |
| 2 |
| 1 |
| 2 |
5-
|
3
| ||
| 5 |
∴tan∠PEO=
| PO |
| OE |
| ||
| 3 |
∴∠PEO=arctan
| ||
| 3 |
| ||
| 3 |
| ||
| 4 |
| ||
| 4 |
(Ⅲ)取PA、PB的中点M、N,连接BM、CN、DM、MN,
∵PC=BC,
∴CN⊥PB①
∵AB⊥BC,且PO⊥AB
∴AB⊥平面PBC
∵CN?平面PBC
∴CN⊥AB②
由①、②知CN⊥平面PAB
由MN∥AB∥CD,MN=AB=CD,得四边形MNCD为平行四边形
∴CN∥DM
∴DM⊥平面PAB
∵BM?平面PAD
∴DM⊥BM
∵PB=AB=2
∴BM⊥PA
∴BM⊥平面PAD,直线PB与平面PAD所成的线面角为∠BPM
在等腰直角三角形PAB中,易知∠BPM=45°
 解法二:(Ⅰ)同解法一;
解法二:(Ⅰ)同解法一;如图,以BC中点O为原点,以BC所在直线为x轴,
过点O与AB平行的直线为y轴,
建立如图所示的空间直角坐标系O-xyz.
(Ⅱ)∵BC=PB=PC=2且PO⊥底面ABCD
∴平面ABCD的法向量为
| OP |
| 3 |
∵A(1,2,0),D(-1,1,0),P(0,0,
| 3 |
∴
| DA |
| PA |
| 3 |
设平面PAD的法向量为
| n1 |
由
|
|
令x1=1,则y1=-2,z3=-
| 3 |
| n1 |
| 3 |
∴cos<
| n1 |
| OP |
| -3 | ||||
|
| ||
| 4 |
∴二面角P-AD-B的大小为arccos
| ||
| 4 |
| ||
| 4 |
| ||
| 3 |
(Ⅲ)∵B(1,0,0)
∴
| PB |
| 3 |
由(Ⅱ)知平面PAD的法向量为
| n1 |
| 3 |
则cos?
| PB |
| n1 |
| ||||
|
|
| 4 | ||
2•2
|
| ||
| 2 |
| PB |
| n1 |
所以直线PB与平面PAD所成的线面角为90°-45°=45°
点评:本题考查直线与平面垂直的判定,二面角的求法,直线与平面所成的角,考查空间想象能力,逻辑思维能力,转化思想,是中档题.

练习册系列答案
相关题目
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC, 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点. 如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2,
如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2, 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1,
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1, 如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=
如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=