题目内容
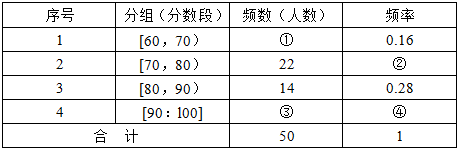
为了让学生更多的了解“数学史”知识,某班级举办一次“追寻先哲的足迹,倾听数学的声音”的数学史知识竞赛活动.现将初赛答卷成绩(得分均为整数,满分为100分)进行统计,制成如下频率分布表:

(Ⅰ)填充频率分布表中的空格(在解答中直接写出对应空格序号的答案);
(Ⅱ)决赛规则如下:为每位参加决赛的选手准备4道判断题,选手对其依次口答,答对两道就终止答题,并获得一等奖,若题目答完仍然只答对1道,则获得二等奖。
某同学进入决赛,每道题答对的概率p的值恰好与频率分布表中不少于80分的频率的值相同。
(ⅰ)求该同学恰好答满4道题而获得一等奖的概率;
(ⅱ)设该同学决定中答题个数为X,求X的分布列及X的数学期望。
(Ⅱ)决赛规则如下:为每位参加决赛的选手准备4道判断题,选手对其依次口答,答对两道就终止答题,并获得一等奖,若题目答完仍然只答对1道,则获得二等奖。
某同学进入决赛,每道题答对的概率p的值恰好与频率分布表中不少于80分的频率的值相同。
(ⅰ)求该同学恰好答满4道题而获得一等奖的概率;
(ⅱ)设该同学决定中答题个数为X,求X的分布列及X的数学期望。
解:(Ⅰ)①8;②0.44;③6;④0.12;
(Ⅱ)由(Ⅰ),得p=0.4,
(ⅰ)该同学恰好答满4道题而获得一等奖,
即前3道题中刚好答对1道,第4道也能够答对才获得一等奖,则有 。
。
(ⅱ)由题设可知,该同学答题个数为2,3,4,即X=2,3,4,

分布列为

∴E(x)=2×0.16+3×0.192+4×0.648=3.488。
(Ⅱ)由(Ⅰ),得p=0.4,
(ⅰ)该同学恰好答满4道题而获得一等奖,
即前3道题中刚好答对1道,第4道也能够答对才获得一等奖,则有
 。
。(ⅱ)由题设可知,该同学答题个数为2,3,4,即X=2,3,4,

分布列为

∴E(x)=2×0.16+3×0.192+4×0.648=3.488。

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
 18、为了让学生更多的了解“数学史”知识,某中学高一年级举办了一次“追寻先哲的足迹,倾听数学的声音”的数学史知识竞赛活动,共有800名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据频率分布表,解答下列问题:
18、为了让学生更多的了解“数学史”知识,某中学高一年级举办了一次“追寻先哲的足迹,倾听数学的声音”的数学史知识竞赛活动,共有800名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据频率分布表,解答下列问题:

 (2011•许昌三模)为了让学生更多的了解“数学史”知识,某中学高二年级举办了一次“追寻先哲的足迹,倾听数学的声音”的数学史知识竞赛活动,共有800名学生参加了这次竞赛.为了解本次竞赛的成绩情况.从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计,请你根据频率分布表,解答下列问题.
(2011•许昌三模)为了让学生更多的了解“数学史”知识,某中学高二年级举办了一次“追寻先哲的足迹,倾听数学的声音”的数学史知识竞赛活动,共有800名学生参加了这次竞赛.为了解本次竞赛的成绩情况.从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计,请你根据频率分布表,解答下列问题.
