题目内容
已知函数 .
.
(Ⅰ)判断函数 的奇偶性; (Ⅱ)求函数
的奇偶性; (Ⅱ)求函数 的单调区间;
的单调区间;
(Ⅲ)若关于 的方程
的方程 有实数解,求实数
有实数解,求实数 的取值范围
的取值范围
【答案】
(Ⅰ)函数 的定义域为{
的定义域为{ 且
且 } ………………… 1分
} ………………… 1分

∴ 为偶函数
………………… 3分
为偶函数
………………… 3分
(Ⅱ)当 时,
时, ………………… 4分
………………… 4分
若 ,则
,则 ,
, 递减;
递减;
若 , 则
, 则 ,
, 递增.
………………… 6分
递增.
………………… 6分
再由 是偶函数,得
是偶函数,得 的递增区间是
的递增区间是 和
和 ;
;
递减区间是 和
和 .
………………… 8分
.
………………… 8分
(Ⅲ)方法一:要使方程 有实数解,即要使函数
有实数解,即要使函数 的图像与直线
的图像与直线 有交点.
函数
有交点.
函数 的图象如图.………………… 9分
的图象如图.………………… 9分

先求当直线 与
与 的图象相切时
的图象相切时 的值.
的值.
当 时,
时, 设切点为
设切点为 ,则切线方程为
,则切线方程为
 ,将
,将 代入,得
代入,得
即 (*)
(*)
显然, 满足(*)
满足(*)
而当 时,
时, ,当
,当
 时,
时,
∴(*)有唯一解 此时
此时
再由对称性, 时,
时, 也与
也与 的图象相切,………………… 13分
的图象相切,………………… 13分
∴若方程 有实数解,则实数
有实数解,则实数 的取值范围是(-∞,-1]∪[1,+∞).
的取值范围是(-∞,-1]∪[1,+∞).
方法二:
由 ,得:
,得: ………………… 9分
………………… 9分
令

当 ,
,
 …………………10分
…………………10分
显然
 时,
时, ,
,
 时,
时, ,
,
∴ 时,
时, ………………… 12分
………………… 12分
又 ,
, 为奇函数
为奇函数
∴ 时,
时,
∴ 的值域为(-∞,-1]∪[1,+∞) …………………
13分
的值域为(-∞,-1]∪[1,+∞) …………………
13分
∴若方程 有实数解,则实数
有实数解,则实数 的取值范围是(-∞,-1]∪[1,+∞).
的取值范围是(-∞,-1]∪[1,+∞).
【解析】略

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目

 (理)已知函数
(理)已知函数
 ,有h(h(a))=a;
,有h(h(a))=a;
 ,使得h(m)=m,若m是函数h(x)的中介元,记
,使得h(m)=m,若m是函数h(x)的中介元,记 时h(x)的中介元为xn,且
时h(x)的中介元为xn,且 ,若对任意的
,若对任意的 ,都有Sn<
,都有Sn<  ,求
,求 的取值范围;
的取值范围; 时,函数y= h(x)的图像总在直线y=1-x的上方,求P的取值范围。
时,函数y= h(x)的图像总在直线y=1-x的上方,求P的取值范围。
 (理)已知函数
(理)已知函数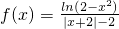 .
.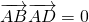 ,求D2+E2-4F的值;
,求D2+E2-4F的值; (λ>-1,p>0)。
(λ>-1,p>0)。 (n∈N+)时h(x)的中介元为xn,且Sn=
(n∈N+)时h(x)的中介元为xn,且Sn= ,若对任意的n∈N+,都有Sn<
,若对任意的n∈N+,都有Sn< ,求λ的取值范围;
,求λ的取值范围;