题目内容
(本题满分9分)已知等比数列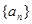 满足
满足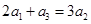 ,且
,且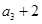 是
是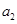 与
与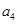 的等差中项;
的等差中项;
(Ⅰ)求数列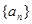 的通项公式; (Ⅱ)若
的通项公式; (Ⅱ)若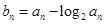 ,
,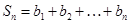 ,
,
求使不等式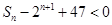 成立的
成立的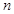 的最小值;
的最小值;
【答案】
(1)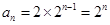 ;(2)
;(2)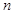 的最小值为
的最小值为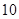 。
。
【解析】(I)设等比数列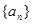 的首项为
的首项为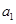 ,公比为
,公比为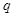 ,根据
,根据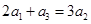 ,且
,且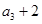 是
是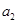 与
与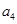 的等差中项建立关于a1和q的方程,求出a1和q的,确定
的等差中项建立关于a1和q的方程,求出a1和q的,确定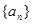 的通项公式.
的通项公式.
(II)在(I)的基础上,可得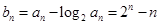 ,然后再采用分组求和的方法求出Sn,再解关于n的不等式
,然后再采用分组求和的方法求出Sn,再解关于n的不等式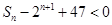 ,解出n的范围,求出n的最小值.
,解出n的范围,求出n的最小值.
解:(1)设等比数列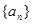 的首项为
的首项为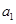 ,公比为
,公比为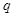 ,
,
则有 ①
① 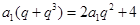 ②
②
由①得: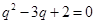 ,解得
,解得 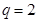 或
或 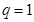 (不合题意舍去)
(不合题意舍去)
当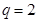 时,代入②得:
时,代入②得: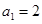 ; 所以
; 所以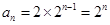 …4分
…4分
(2)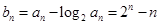
所以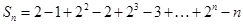
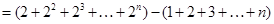
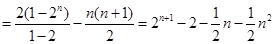 …7分
…7分
因为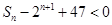 代入得
代入得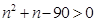 , 解得
, 解得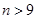 或
或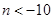 (舍去)
(舍去)
所以所求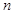 的最小值为
的最小值为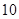 …9分
…9分

练习册系列答案
相关题目
 :函数
:函数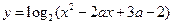 的定义域为R;命题
的定义域为R;命题 :方程
:方程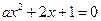 有两个不相等的负数根,若
有两个不相等的负数根,若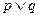 是假命题,求实数
是假命题,求实数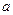 的取值范围
的取值范围 轴上的抛物线过点
轴上的抛物线过点 .
. 作直线交抛物线于
作直线交抛物线于 两点,使得
两点,使得 恰好平分线段
恰好平分线段 ,求直线
,求直线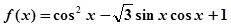 .
.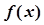 的单调递增区间;
的单调递增区间;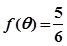 ,
,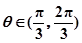 ,求
,求 的值;
的值;  ,
,

