题目内容
若定义在区间 上的函数
上的函数 满足:对于任意的
满足:对于任意的 ,都有
,都有 ,且
,且 时,有
时,有 ,
, 的最大值、最小值分别为
的最大值、最小值分别为 ,则
,则 的值为( )
的值为( )
| A.2012 | B.2013 | C.4024 | D.4026 |
C
解析试题分析:令 ,所以
,所以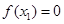 .即
.即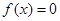 .再令
.再令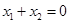 .代入可得
.代入可得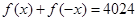 .设
.设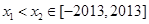 .
.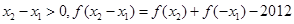 所以
所以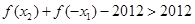 .又因为
.又因为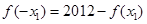 .所以可得
.所以可得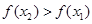 .所以可得函数是递增.所以
.所以可得函数是递增.所以 .又因为
.又因为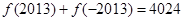 .故选C.
.故选C.
考点:1.函数的单调性.2.函数的特殊值法寻找等量关系.3.等式与不等式间的互化.4.归纳化归的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知 是方程
是方程 的两根,且
的两根,且 ,
, ,
, ,求
,求 的最大值与最小值之和为( ).
的最大值与最小值之和为( ).
| A.2 | B. | C. | D.1 |
已知函数 ,若
,若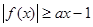 恒成立,则实数a的取值范围是( )
恒成立,则实数a的取值范围是( )
A.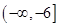 | B. |
C. | D. |
设 ,
, ,
, ,则
,则 的大小顺序为( )
的大小顺序为( )
A. | B. | C. | D. |
函数 的零点所在区间是( )
的零点所在区间是( )
A. | B. | C. | D. |
如果二次函数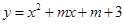 不存在零点,则
不存在零点,则 的取值范围是( )
的取值范围是( )
A. | B. |
C. | D. |
函数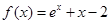 的零点所在的区间为
的零点所在的区间为
| A.(-2,-l) | B.(-1,0) |
| C.(0,1) | D.(1,2) |
已知函数f(x)= 若关于x的方程f(f(x))=0有且仅有一个实数解,则实数a的取值范围是( )
若关于x的方程f(f(x))=0有且仅有一个实数解,则实数a的取值范围是( )
| A.(-∞,0) | B.(-∞,0)∪(0,1) |
| C.(0,1) | D.(0,1)∪(1,+∞) |
设函数f(x)=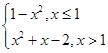 则f
则f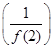 的值为( ).
的值为( ).
A.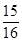 | B.-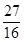 | C.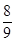 | D.18 |