题目内容
 函数f(x)=ax3+bx2+cx+d图象如右图,若函数
函数f(x)=ax3+bx2+cx+d图象如右图,若函数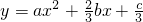 在区间[|m-1|,+∞)上单调递增,则实数m的取值范围是
在区间[|m-1|,+∞)上单调递增,则实数m的取值范围是
- A.
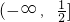
- B.
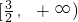
- C.

- D.
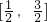
C
分析:由函数f(x)=ax3+bx2+cx+d图象,知-2,3是f′(x)=3ax2+2bx+c的根,且a>0. ,故
,故 ,c=-18a,所以函数
,c=-18a,所以函数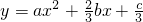 =a(x2-x-6),由y′=2ax-a,知函数
=a(x2-x-6),由y′=2ax-a,知函数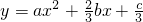 的增区间是[
的增区间是[ ,+∞),故[|m-1|,+∞)⊆[
,+∞),故[|m-1|,+∞)⊆[ ),由此能求出m的范围.
),由此能求出m的范围.
解答:由函数f(x)=ax3+bx2+cx+d图象,知-2,3是函数f(x)的极值点,
∴-2,3是f′(x)=3ax2+2bx+c的根,且a>0.
∴ ,∴
,∴ ,c=-18a,
,c=-18a,
∴函数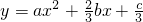 =a(x2-x-6),
=a(x2-x-6),
∴y′=2ax-a,
∵a>0,∴由y′=2ax-a>0,得x> ,
,
∴函数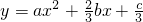 的增区间是[
的增区间是[ ,+∞),
,+∞),
∵函数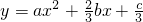 在区间[|m-1|,+∞)上单调递增,
在区间[|m-1|,+∞)上单调递增,
∴[|m-1|,+∞)⊆[ ),
),
解得m∈ .
.
故选C.
点评:本题考查利用导数求闭区间上函数最值的应用,综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答,注意合理地进行等价转化.
分析:由函数f(x)=ax3+bx2+cx+d图象,知-2,3是f′(x)=3ax2+2bx+c的根,且a>0.
 ,故
,故 ,c=-18a,所以函数
,c=-18a,所以函数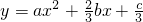 =a(x2-x-6),由y′=2ax-a,知函数
=a(x2-x-6),由y′=2ax-a,知函数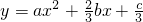 的增区间是[
的增区间是[ ,+∞),故[|m-1|,+∞)⊆[
,+∞),故[|m-1|,+∞)⊆[ ),由此能求出m的范围.
),由此能求出m的范围.解答:由函数f(x)=ax3+bx2+cx+d图象,知-2,3是函数f(x)的极值点,

∴-2,3是f′(x)=3ax2+2bx+c的根,且a>0.
∴
 ,∴
,∴ ,c=-18a,
,c=-18a,∴函数
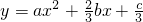 =a(x2-x-6),
=a(x2-x-6),∴y′=2ax-a,
∵a>0,∴由y′=2ax-a>0,得x>
 ,
,∴函数
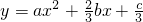 的增区间是[
的增区间是[ ,+∞),
,+∞),∵函数
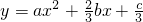 在区间[|m-1|,+∞)上单调递增,
在区间[|m-1|,+∞)上单调递增,∴[|m-1|,+∞)⊆[
 ),
),解得m∈
 .
.故选C.
点评:本题考查利用导数求闭区间上函数最值的应用,综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目