题目内容
已知函数f(x)=ln2(1+x)- 。
。
(1)求函数f(x)的单调区间;
(2)若不等式(1+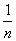 )n+a≤e对任意的n∈N*都成立(其中e是自然对数的底数)。求a的最大值。
)n+a≤e对任意的n∈N*都成立(其中e是自然对数的底数)。求a的最大值。
 。
。(1)求函数f(x)的单调区间;
(2)若不等式(1+
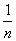 )n+a≤e对任意的n∈N*都成立(其中e是自然对数的底数)。求a的最大值。
)n+a≤e对任意的n∈N*都成立(其中e是自然对数的底数)。求a的最大值。解:(1)函数f(x)的定义域是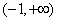
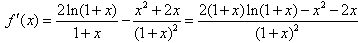
设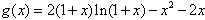
则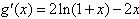
令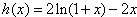
则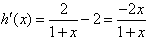
当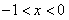 时,
时,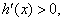
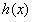 在(-1,0)上为增函数
在(-1,0)上为增函数
当x>0时,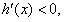
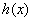 在
在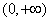 上为减函数
上为减函数
所以h(x)在x=0处取得极大值,而h(0)=0
所以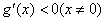
函数g(x)在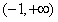 上为减函数
上为减函数
于是当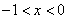 时,
时,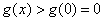
当x>0时,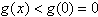
所以,当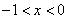 时,
时,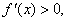
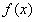 在(-1,0)上为增函数
在(-1,0)上为增函数
当x>0时,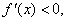
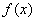 在
在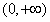 上为减函数
上为减函数
故函数f(x)的单调递增区间为(-1,0),单调递减区间为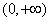 。
。
(2)不等式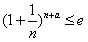 等价于
等价于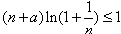
由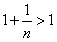 知
知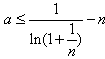
设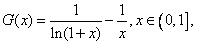
则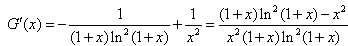
由(1)知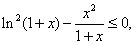 即
即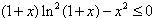
所以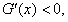
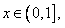 于是G(x)在
于是G(x)在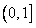 上为减函数
上为减函数
故函数G(x)在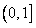 上的最小值为
上的最小值为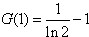
所以a的最大值为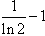 。
。
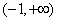
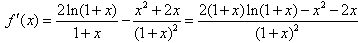
设
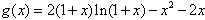
则
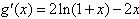
令
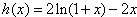
则
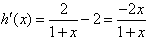
当
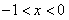 时,
时,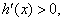
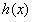 在(-1,0)上为增函数
在(-1,0)上为增函数当x>0时,
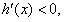
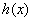 在
在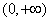 上为减函数
上为减函数所以h(x)在x=0处取得极大值,而h(0)=0
所以
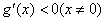
函数g(x)在
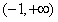 上为减函数
上为减函数于是当
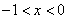 时,
时,当x>0时,
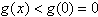
所以,当
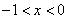 时,
时,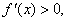
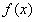 在(-1,0)上为增函数
在(-1,0)上为增函数当x>0时,
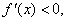
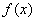 在
在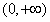 上为减函数
上为减函数故函数f(x)的单调递增区间为(-1,0),单调递减区间为
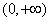 。
。(2)不等式
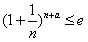 等价于
等价于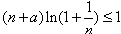
由
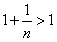 知
知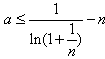
设
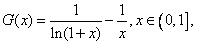
则
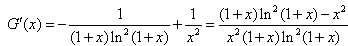
由(1)知
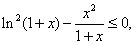 即
即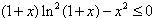
所以
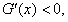
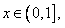 于是G(x)在
于是G(x)在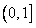 上为减函数
上为减函数故函数G(x)在
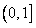 上的最小值为
上的最小值为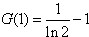
所以a的最大值为
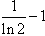 。
。
练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目