题目内容
不等式3 x2＞3-x+2的解集是
（-∞，-2）∪（1，+∞）
（-∞，-2）∪（1，+∞）
．分析：由不等式3 x2＞3-x+2可得 x2＞-x+2，即 （x+2）（x-1）＞0，解此一元二次不等式求得原不等式的解集．
解答：解：由不等式3 x2＞3-x+2可得 x2＞-x+2，即 （x+2）（x-1）＞0．
求得x＜-2，或x＞1，即 x∈（-∞，-2）∪（1，+∞），
故答案为 （-∞，-2）∪（1，+∞）．
求得x＜-2，或x＞1，即 x∈（-∞，-2）∪（1，+∞），
故答案为 （-∞，-2）∪（1，+∞）．
点评：本题主要考查指数函数的单调性和特殊点，指数不等式的解法，属于中档题．
练习册系列答案
相关题目
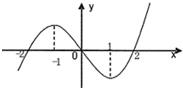9、已知R上可导函数f（x）的图象如图所示，则不等式（x2-2x-3）f′（x）＞0的解集为（ ）