题目内容
(2011•顺义区二模)给定集合A,若对于任意a,b∈A,有a+b∈A,且a-b∈A,则称集合A为闭集合,给出如下四个结论:
①集合A={-4,-2,0,2,4}为闭集合;
②集合A={n|n=3k,k∈Z}为闭集合;
③若集合A1,A2为闭集合,则A1∪A2为闭集合;
④若集合A1,A2为闭集合,且A1⊆R,A2⊆R,则存在c∈R,使得c∉(A1∪A2).
其中正确结论的序号是
①集合A={-4,-2,0,2,4}为闭集合;
②集合A={n|n=3k,k∈Z}为闭集合;
③若集合A1,A2为闭集合,则A1∪A2为闭集合;
④若集合A1,A2为闭集合,且A1⊆R,A2⊆R,则存在c∈R,使得c∉(A1∪A2).
其中正确结论的序号是
②④
②④
.分析:本题考查的是新定义和集合知识综合的问题,在解答时首先要明确闭集合是什么,然后严格按照题目当中对“闭集合”的定义逐一验证即可.
解答:解:对于①:-4+(-2)=-6∉A,故不是闭集合,故错;
对于②:由于任意两个3的倍数,它们的和、差仍是3 的倍数,故是闭集合,故正确;
对于③:假设A1={n|n=3k,k∈Z},A2={n|n=5k,k∈Z},3∈A1,5∈A2,但是,3+5∉A1∪A2,则A1∪A2不是闭集合,故错.
对于④:设集合A1=A2=R,都为闭集合,但不存在c∈R,使得c∉(A1∪A2);故④错误.
正确结论的序号是②④.
故答案为:②④.
对于②:由于任意两个3的倍数,它们的和、差仍是3 的倍数,故是闭集合,故正确;
对于③:假设A1={n|n=3k,k∈Z},A2={n|n=5k,k∈Z},3∈A1,5∈A2,但是,3+5∉A1∪A2,则A1∪A2不是闭集合,故错.
对于④:设集合A1=A2=R,都为闭集合,但不存在c∈R,使得c∉(A1∪A2);故④错误.
正确结论的序号是②④.
故答案为:②④.
点评:本题考查的是集合知识和新定义的问题.在解答过程当中应充分体会新定义问题概念的确定性,与集合子集个数、子集构成的规律.此题综合性强,值得同学们认真总结和归纳.

练习册系列答案
相关题目
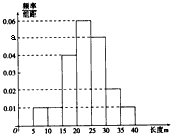 (2011•顺义区二模)某棉纺厂为了解一批棉花的质量,从中随机抽测100根棉花纤维的长度(棉花纤维的长度是棉花质量的重要指标).所得数据均在区间[5,40]中,其频率分布直方图如图所示,由图中数据可知a=
(2011•顺义区二模)某棉纺厂为了解一批棉花的质量,从中随机抽测100根棉花纤维的长度(棉花纤维的长度是棉花质量的重要指标).所得数据均在区间[5,40]中,其频率分布直方图如图所示,由图中数据可知a=