题目内容
16.已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1,(a>b>0)的左、右焦点分别为F1,F2,P是短轴的一个顶点,△PF1F2是顶角为$\frac{2}{3}$π且面积为$\sqrt{3}$的等腰三角形.(1)求椭圆的标准方程;
(2)过点A(-a,0)斜率为k的直线交椭圆于点B.直线BO(O为坐标原点)交椭圆于另一点C.若$k∈[\frac{1}{2},1]$,求△ABC的面积的最大值.
分析 (1)由题意可得a=2b,c=$\sqrt{3}$b,运用三角形的面积公式,计算可得a,b,进而得到椭圆方程;
(2)设直线AB的方程为x+2=my(m=$\frac{1}{k}$),代入椭圆方程,求得B的坐标,由题意可得C的坐标,求出△ABC的面积,运用对勾函数的单调性,即可得到最大值.
解答 解:(1)由题意可得a=2b,c=$\sqrt{3}$b,
△PF1F2的面积S=$\frac{1}{2}$•2$\sqrt{3}$b•b=$\sqrt{3}$,
得b=1,c=$\sqrt{3}$,a=2,
所以椭圆的标准方程为$\frac{{x}^{2}}{4}$+y2=1;
(2)设直线AB的方程为x+2=my(m=$\frac{1}{k}$)
代入椭圆方程得(m2+4)y2-4my=0,
可得B($\frac{2{m}^{2}-8}{{m}^{2}+4}$,$\frac{4m}{4+{m}^{2}}$),C(-$\frac{2{m}^{2}-8}{4+{m}^{2}}$,-$\frac{4m}{4+{m}^{2}}$)
△ABC的面积S=$\frac{1}{2}$•2•$\frac{8m}{4+{m}^{2}}$=$\frac{8}{m+\frac{4}{m}}$,
令f(m)=m+$\frac{4}{m}$,f′(m)=1-$\frac{4}{{m}^{2}}$(1≤m≤2),
f′(m)≤0,f(m)=m+$\frac{4}{m}$在[1,2]上单调递减,
所以当m=2时,△ABC的面积的最大值为2.
点评 本题考查椭圆的方程和性质,主要考查椭圆方程的运用,联立直线方程,求得交点,同时考查三角形的面积公式和对勾函数的单调性的运用,属于中档题.

练习册系列答案
相关题目
6.一直集合M={(x,y)|y=x2+1},N={(x,y)|y=x+1},则M∩N=( )
| A. | (0,1),(1,2) | B. | {(0,1),(1,2)} | C. | {y|y=1或y=2} | D. | {y|y≥1} |
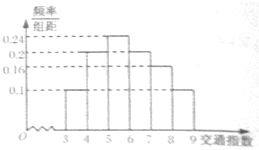 交通指数是交通拥堵指数的简称,是综合反映道路间畅通或拥堵的概念.记交通指数为T.其范围为[0,10],分别有五个级别:T∈[0,2)畅通;T∈[2,4)基本畅通; T∈[4,6)轻度拥堵; T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3),从郑州市交通指挥中心随机选取了三环以内的50个交通路段,依据其交通指数数据绘制的频率分布直方图如图 所示:
交通指数是交通拥堵指数的简称,是综合反映道路间畅通或拥堵的概念.记交通指数为T.其范围为[0,10],分别有五个级别:T∈[0,2)畅通;T∈[2,4)基本畅通; T∈[4,6)轻度拥堵; T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3),从郑州市交通指挥中心随机选取了三环以内的50个交通路段,依据其交通指数数据绘制的频率分布直方图如图 所示: 如图1在直角三角形ABC中,∠A=90°,AB=2,AC=4,D,E分别是AC,BC边上的中点,M为CD的中点,现将△CDE沿DE折起,使点A在平面CDE内的射影恰好为M.
如图1在直角三角形ABC中,∠A=90°,AB=2,AC=4,D,E分别是AC,BC边上的中点,M为CD的中点,现将△CDE沿DE折起,使点A在平面CDE内的射影恰好为M.